2013
- 92
- 0
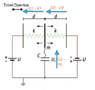
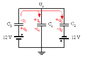
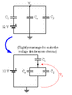
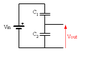
The capacitors are switched in series and I wanted to determine the total capacity to come up with the extra capacity over the load.
How do I do that then?
How do I do that then?