Saladsamurai
- 3,009
- 7
[SOLVED] Seriously? Moment of Force about a specified Axis
So I really thought I understood this. I have attached the problem and attempt at solution. It should be easy to follow. Problem
Attempt at Solution
This was my process:
1. Write each F and each r as cartesian vectors
2. Find each moment by cross product.
3. Add the moments to get resultant moment M_R. Find unit vector along Oa axis=U_oa
4. Use resultant Moment and Unit vector along Oa to find
M_R dot U_oa=|M_oa|
5. Write as Cartesian vector-->|M_oa|*U_oa
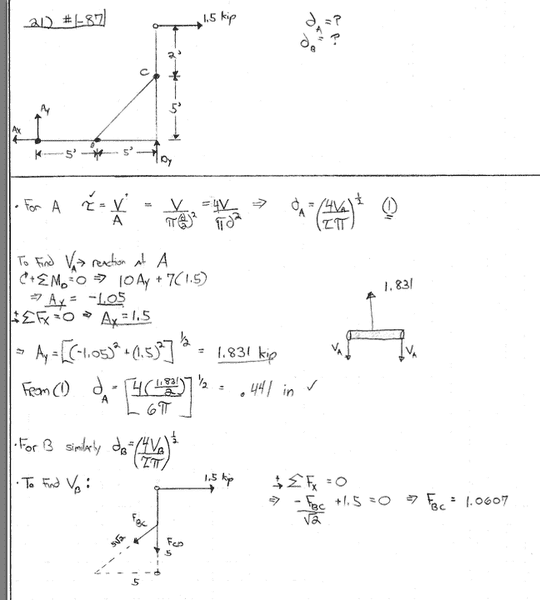
The answer is supposed to be 26.1i-15.1j lb*ft. As you can see, my answer isn't close (WTF else is new!)
What is wrong with my method?
Thanks,
Casey
So I really thought I understood this. I have attached the problem and attempt at solution. It should be easy to follow. Problem
Attempt at Solution
This was my process:
1. Write each F and each r as cartesian vectors
2. Find each moment by cross product.
3. Add the moments to get resultant moment M_R. Find unit vector along Oa axis=U_oa
4. Use resultant Moment and Unit vector along Oa to find
M_R dot U_oa=|M_oa|
5. Write as Cartesian vector-->|M_oa|*U_oa
The answer is supposed to be 26.1i-15.1j lb*ft. As you can see, my answer isn't close (WTF else is new!)
What is wrong with my method?
Thanks,
Casey