physea
- 211
- 3
Hello
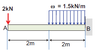
I am a bit confused how to calculate the shear force and bending moment graph for a beam under point loads, distributed loads and bending moments.
Is the discontinuous functions the best method to solve such problems?
Can anyone outline an approach?
I don't understand for example how to divide the loads in regions etc.
Thanks
I am a bit confused how to calculate the shear force and bending moment graph for a beam under point loads, distributed loads and bending moments.
Is the discontinuous functions the best method to solve such problems?
Can anyone outline an approach?
I don't understand for example how to divide the loads in regions etc.
Thanks