tonyjk
- 227
- 3
hello all... Please can i know physically why the pressure drop in a fluid when there's shear stress? what happens? thank you
The discussion centers on the relationship between shear stress and pressure drop in fluids, clarifying misconceptions about fluid mechanics. It is established that fluids can exhibit shear stress due to viscosity, as described by Newton's law of viscosity. The pressure drop in a pipe is directly related to the shear stress at the wall, with the formula for laminar flow being pressure drop equal to 4L/D times the shear stress. The conversation also addresses the concept of ideal fluids, emphasizing that they are theoretical constructs with negligible viscosity, resulting in no pressure drop.
PREREQUISITESStudents and professionals in fluid mechanics, mechanical engineers, and anyone involved in the design and analysis of fluid systems, particularly in understanding pressure dynamics in piping systems.
davenn said:Greetings Tonyik
Firstly
you cannot have shear stress in a fluid ... That is, fluids cannot support shear stress
This is how we found out that the outer core of the Earth is liquid, because earthquake shear waves will not propagate through that region
knowing that, would you like to redefine your question and maybe give an example relating to your question
cheers
Dave
Chestermiller said:Of course you can have shear stress in a fluid. According to Newton's law of viscosity, for a fluid that is being sheared between parallel plates, the shear stress is equal to the viscosity times the shear rate, with the shear rate equal to the relative velocity divided by the distance between the plates.
In a fluid flowing through a pipe, there is a viscous shear stress at the wall that acts in the direction opposite to the direction of fluid motion. This integrates to a tangential force at the wall. In order to overcome this force, you need a higher pressure at the inlet of the pipe than at the exit. For pipe flow, the pressure drop in the pipe is equal to 4L/D times the shear stress at the wall, where L is the length of the pipe and D is the diameter. The shear stress at the wall for laminar flow is equal to 8V/D times the viscosity, where V is the volumetric average velocity of the fluid.
If you want to learn more about this, see Transport Phenomena by Bird, Stewart, and Lightfoot.
Chet
Who said anything about gasses and liquids supporting shear strain? You do know the difference between stress and strain, correct? The OP was asking about shear stresses in a liquid, and how they contribute to pressure drop. Either your lecturer didn't know much about fluid mechanics, or you misinterpreted what he was saying. Viscosity is precisely what we are talking about here. This is the fluid property that allows a fluid to develop shear stress. I hope you really didn't think that shear stresses could only exist in solids. In a liquid, the shear stress is proportional to the rate of strain, rather than the strain itself.davenn said:my geophysics lecturer at university would have severely debated that with you
and would have give you the inverted jug of beer experiment to prove otherwise
if a fluid could support shearing then why do shear waves not travel through it ?
it just doesn't happen, Shear modulus of a fluid = 0
shear modulus
Shear Modulus (S) also known as the rigidity modulus
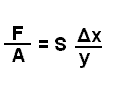
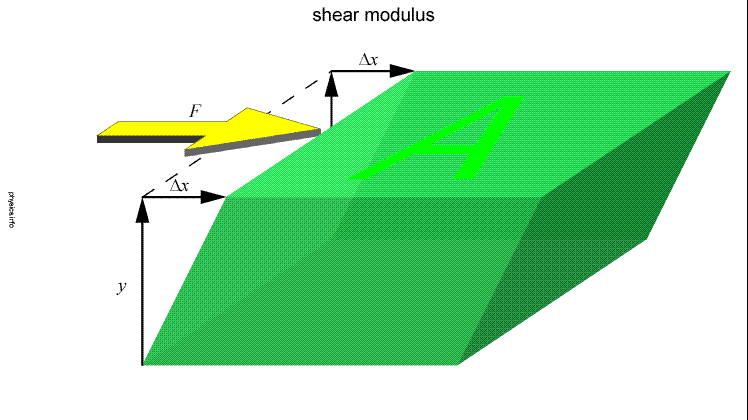
Gases and liquids can not have shear moduli. They have viscosity instead.
http://physics.info/elasticity/Dave
i mean why the viscous forces causes pressure drop in a molecular view that's what i mean by physically... thanks again"The need for the pressure drop can be viewed from two different standpoints. In terms of a force balance, the pressure force is needed to overcome the viscous forces generated. In terms of an energy balance, the work done by the pressure force is needed to overcome the viscous dis- sipation of energy throughout the fluid"
Chestermiller said:If you want to learn more about this, see Transport Phenomena by Bird, Stewart, and Lightfoot.
Chet
But in fluid flow, DP is used to designate pressure drop, and thus it is P1 - P2
. A pressure drop due to viscous
effects represents an irreversible pressure loss, and it is called pressure loss
DPL to emphasize that it is a loss (just like the head loss hL
Note from Eq. 8–20 that the pressure drop is proportional to the viscosity
u of the fluid, and DP would be zero if there were no friction. Therefore,
the drop of pressure from P1 to P2 in this case is due entirely to viscous
effects
tonyjk said:sorry for re-openning this thread but really I am not getting it look what i found:
Im confused about why they call it a pressure loss? if it's necessary for a pressure drop in a fluid to flow in a pipe than why they called it pessure loss? and why they say if there's no friction there's no pressure drop? so how can an ideal fluid even in theory flow without a pressure drop... thanks again
http://www.uio.no/studier/emner/matnat/math/MEK4450/h11/undervisningsmateriale/modul-5/Pipeflow_intro.pdf even all the books they say its a pressure loss..