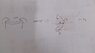- #1
fonseh
- 529
- 2
Homework Statement
We all know that $$\tau = VQ/ It $$
how to determine the shear stress at **G** ?
I'm having problem of finding Ay
centroid if the solid that i found earlier is y = 98.5mm
There's a dashed line from G to the bottom . It's making me confused . for Q , should i consider the area either to the left or right of the G ? like the red and orange part
Homework Equations
The Attempt at a Solution
so , my working is
Q = Ay = (250x10^-3)(50x10^-3)( 50+125-98)(10^-3) = 9.63x10^-4
Is my concept correct ?
I'm considering the area above the G .
[/B]