- #1
portofino
- 35
- 0
Homework Statement
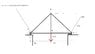
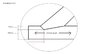
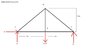
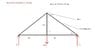
member AD of the timber truss shown (attached) is framed into the 100 X 50 -mm bottom chord ABC as shown (attached - detailed view). determine the dimension 'a' that must be used if the average shearing stress parallel to the grain at the ends of the chord ABC is not to exceed 2.25 MPa
Homework Equations
shearing stress, tau = V/A where V is shear force, A is cross sectional area --> average
The Attempt at a Solution
is my free body diagram correct? if so, do i first solve for the forces in each member using the method of joints. do i consider that the chord in question is also the same at where the roller is located?
once i have found all the forces in each member based on the free body diagram do i just use what i found to be the force at C as the value for V in the shearing stress formula? do i then just solve for A aka 'a'?
please tell me if i am on the right track, if not, any assistance appreciated