- #1
Fischer777
- 89
- 1
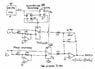
For a school project I need to be able to shift the phase of a 100 kHz sine wave by 90 degrees (either positive or negative). I have tried several passive integrators and differentiators, both with poor results. I have also tried using an op-amp integrator and differentiator, but in both cases I got a heavily distorted waveform that didn't seem to be 90 degrees shifted. I'm running out of ideas, so I'm wondering if anyone here has some pointers or tips for building a relatively simple circuit for a phase shift.
Thanks!
Thanks!