Should I consider internal forces for this hinged structure?

[Mech_LS24]

Summary:: A hinged structure applied with a load, should the structure totally been calculated in order to find the resultant force?

Hello,

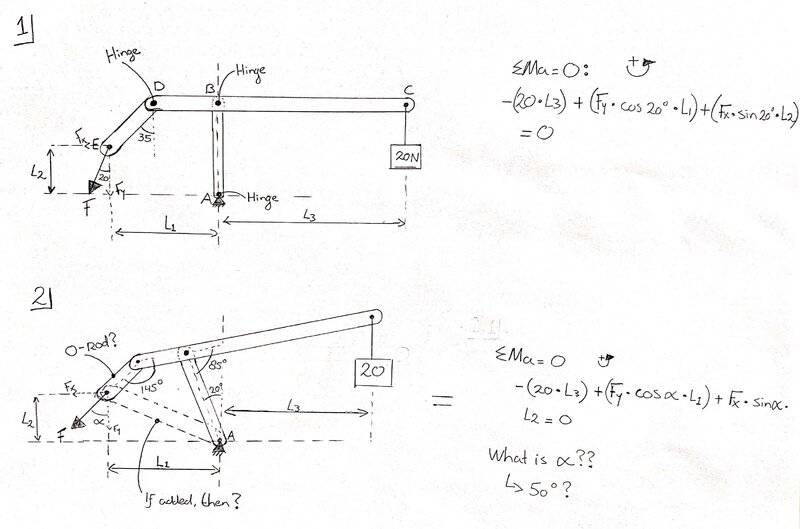
Two situations, the first is a simple structure with a 20 N load at point C. The moment-equation is composed next to it.

Second situation:
A hinged structure is again loaded with 20 N. A moment-equation can also been found next to it.

For both situations,

• Are the moment-equations correct? Or should I take internal forces also in consideration?
• Would a 'extra' rod drawn in situation 2 affect the moment-equation?
• Could situation 2 be simplified? I was thinking about kind of a 0-rod (see sketch). That is in line with the force so it actually does nothing more than passing a force.

Mentor note: Moved from engineering forum, so no template.

 

[willem2]

The momentum equation is fine, but how dit you determine the direction of F? If E is a pin joint, DE will rotate until it is in the line of F.

Same question for situation 2. If F is in the same direction as DE, the new rod has no forces. if E is a pin joint this should happen. If you don't know what α is, you can't solve it.

 

[Mech_LS24]

The momentum equation is fine, but how dit you determine the direction of F?

I see, I think I made a mistake there. Force F should be vertically down instead, this would make more sense.

If F is in the same direction as DE, the new rod has no forces. if E is a pin joint this should happen.

This makes sense :). That would make rod AE a 0-rod.

With this information, I think I can say the internal forces doesn't need to be considered. If I want to calculate the needed Force F, I can apply a moment-equation about point A?