Sign Convention for Angular Acceleration in Rotational Motion

[Santilopez10]

Homework Statement

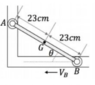
Point B of a rod of lenght 0.46 m has a constant velocity of 2 m/s to the left. If $\theta = \frac{\pi}{4}$, find:
a) The angular velocity and acceleration of the rod.
b) The acceleration of the center of mass.

Relevant Equations

Rigid body kinematics

we know that the center of instantaneous 0 velocity lies in the interception of 2 perpendicular lines to 2 points, which in this case lies above B. The velocity of any point of the rod can be described relative to the center of instantaneuous 0 velocity $(Q)$ as: $$\vec v_{P/Q}=\vec \omega \times \vec r_{P/Q}$$ For our problem, $\vec v_{B/Q}=-2 \hat i$ ,$\vec r_{B/Q}=-0.46 \sin {\frac{\pi}{4}} \hat j=-0.33 \hat j$ and $\vec \omega = \omega \hat k$ (We will not assume its sign). Then $$-2 \hat i = 0.33 \omega \hat i \rightarrow \omega = -6 \rightarrow \vec \omega=-6 \hat k$$ This seems physically correct as the rod is rotating clockwise. Before we obtain the angular acceleration we need the velocity of point A, which we can relate to B as $\vec v_{A/O}=\vec v_{B} + \vec \omega \times \vec r_{A/B}$ (Where O is a fixed stationary origin) which ends up being $\vec v_{A/O}=2 \hat j$.
Let's try to find the acceleration of point A, the equation relating the acceleration of A to B` s is: $$ \vec a_{A/O}= \vec a_{B/O}+ \vec \alpha \times \vec r_{A/B} + \vec \omega \times \vec v_{A/B}$$.
For our case B moves with constant velocity at that instant, $\vec \alpha = \alpha \hat k$, $\vec r_{A/B} = -0.33 \hat i +0.33 \hat j$, $\vec a_{A/O}= a \hat j$ and $\vec v_{A/B} = 2 \hat i + 2 \hat j$. After doing the calculations we arrive at a system of equations: $$
\begin{cases}
-0.33 \alpha +12 =0 \\
-0.33 \alpha -12= a
\end{cases} $$
For which only we are interested in the first. From there we obtain that $\vec \alpha = 36.36 \hat k$. Here raises my question. Should $\vec \alpha$ be negative for this situation? Or is a positive answer physically correct?

 

[haruspex]

$\vec r_{A/B} = -0.33 \hat i +0.33 \hat j$

Check that.

Your -6 for angular velocity seems a little inaccurate, and you should specify units.

 

[Santilopez10]

Check that.

Your -6 for angular velocity seems a little inaccurate, and you should specify units.

A/B means “A respect to B”, maybe I was not so clear. Otherwise I do not know what's the problem. $\cos{\frac{\pi}{4}} 0.46=0.33$ same for sin. Then A is located -0.33 meters to the left and 0.33 meters upwards.

 

[haruspex]

A/B means “A respect to B”, maybe I was not so clear. Otherwise I do not know what's the problem. $\cos{\frac{\pi}{4}} 0.46=0.33$ same for sin. Then A is located -0.33 meters to the left and 0.33 meters upwards.

Sorry, my mistake.
Using a very different approach I got an angular acceleration of -26.7 rad s^-2. I'm pretty sure it should be negative. As the rod rises from the horizontal, the angular velocity starts at plus infinity and reduces to 2/.46 at the vertical.

Edit: no, no, no. It starts at minus infinity, so a positive angular acceleration is correct!

 

[Santilopez10]

Sorry, my mistake.
Using a very different approach I got an angular acceleration of -26.7 rad s^-2. I'm pretty sure it should be negative. As the rod rises from the horizontal, the angular velocity starts at plus infinity and reduces to 2/.46 at the vertical.

Care to show your approach?

 

[haruspex]

Care to show your approach?

JUst used Cartesian coordinates, $x=L\cos(\theta)$ etc.
Got $\omega=\frac v{L\sin(\theta)}$ and hence $\dot\omega=-\frac{v}{L\sin^2(\theta)}\omega=-\frac{v^2}{L^2\sin^3(\theta)}$. That gives -53.4, double what I said before.

 

[Santilopez10]

I believe you missed the linear acceleration term that arises due to the quotient rule. Plus the derivative of 1/sin(x) is not 1/sin^2(x).

 

[haruspex]

I believe you missed the linear acceleration term that arises due to the quotient rule. Plus the derivative of 1/sin(x) is not 1/sin^2(x).

I don't think I missed a linear acceleration term; I did use that $\ddot x=0$. But You are right about the other - I did drop a cos. Careless.
So now I get -37.8, very close to yours, except for the sign.

 

[Santilopez10]

Seems like compared to your answer, the term that is giving me problems is $\vec \omega \times \vec v_{A/B}$. If only $\vec v_{A/B}$ would be $-2 \hat i + 2 \hat j$ instead of $2 \hat i + 2 \hat j$ then I could get the negative sign. To be honest I do not see where I committed a mistake.

 

[haruspex]

Seems like compared to your answer, the term that is giving me problems is $\vec \omega \times \vec v_{A/B}$. If only $\vec v_{A/B}$ would be $-2 \hat i + 2 \hat j$ instead of $2 \hat i + 2 \hat j$ then I could get the negative sign. To be honest I do not see where I committed a mistake.

I have now stepped through your method. In the first of your final pair of equations (the $\hat i$ equation) I get -12, not +12. If still stuck, please post all the steps.

Edit: cancel that - yet another mistake by me.

Btw, I strongly recommend working entirely algebraically, not plugging in any numbers until the final step. It has many advantages, including better precision and readability for others.

 

[Santilopez10]

I have now stepped through your method. In the first of your final pair of equations (the $\hat i$ equation) I get -12, not +12. If still stuck, please post all the steps.

Btw, I strongly recommend working entirely algebraically, not plugging in any numbers until the final step. It has many advantages, including better precision and readability for others.

$$a \hat j= \alpha \hat k \times (-0.33 \hat i + 0.33 \hat j) -6 \hat k \times (2 \hat i + 2 \hat j)$$
$$-6 \hat k \times (2 \hat i + 2 \hat j)=
\begin{vmatrix}
i & j & k \\
0 & 0 & -6 \\
2 & 2 & 0
\end{vmatrix} =6
\begin{vmatrix}
i & j \\
2 & 2
\end{vmatrix} = 12 \hat i -12 \hat j$$
then in the $\hat i$ equation I get +12.

 

[haruspex]

$$a \hat j= \alpha \hat k \times (-0.33 \hat i + 0.33 \hat j) -6 \hat k \times (2 \hat i + 2 \hat j)$$
$$-6 \hat k \times (2 \hat i + 2 \hat j)=
\begin{vmatrix}
i & j & k \\
0 & 0 & -6 \\
2 & 2 & 0
\end{vmatrix} =6
\begin{vmatrix}
i & j \\
2 & 2
\end{vmatrix} = 12 \hat i -12 \hat j$$
then in the $\hat i$ equation I get +12.

Yes, you are right again, it is +12. But I think I have it... Please see my edit to post #4.

(I can't believe I made so many blunders in one thread. I may have to hand back my award.)

 

[Santilopez10]

Yes, you are right again, it is +12. But I think I have it... Please see my edit to post #4.

(I can't believe I made so many blunders in one thread. I may have to hand back my award.)

Alright, but then why when using parametrization we get a negative answer?

 

[Santilopez10]

JUst used Cartesian coordinates, $x=L\cos(\theta)$ etc.
Got $\omega=\frac v{L\sin(\theta)}$ and hence $\dot\omega=-\frac{v}{L\sin^2(\theta)}\omega=-\frac{v^2}{L^2\sin^3(\theta)}$. That gives -53.4, double what I said before.

You missed a negative sign in the expression for $\omega$ which arises from the derivative of cosine.

 

[Santilopez10]

bump.

 

[haruspex]

You missed a negative sign in the expression for $\omega$ which arises from the derivative of cosine.

Yes, I was rather careless wasn't I.
Thanks.