Sign of moment in buckling of column

[fonseh]

Homework Statement

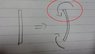
Can someone explain why the M is assigned to be anticlockwise here ?

Homework Equations

The Attempt at a Solution

When i assign it as clockwise , i will get -P(δ -v) , which is different from the author ... Can i do so ? Why ?

 

[fonseh]

for the second example here , i can understand that M = -Pv , since M+Pv = 0 at either end when it's in equlibrium. ( I have showed in the working)

P/s : I know the the sign convention of the bending moment of beam is positive when the beam upwards as shown ...

For the first example in post#1 , i gt M+P(∂-v) = 0 , so M = - P(∂-v) .
I am not sure whether is my concept correct or not . My working is in the 3rd photo here

 

[fonseh]

Is my concept wrong ? can someone explain it ?

 

[PhanthomJay]

Draw a FBD appropriately of an arbitrary cut section of the top part of the deflected column and determine the direction and magnitude of the moment of the applied force P. What must be the direction and magnitude of the internal moment at the cut?

 

[CivilSigma]

The moment M has to be counter clock wise at the base because from the given figure the applied force P will try and rotate the column clockwise

 

[fonseh]

The moment M has to be counter clock wise at the base because from the given figure the applied force P will try and rotate the column clockwise

How about the case in post#2 ? Why
M = -Pv ? For this case , why the M at the bottom = clockwise? since to balance the anticlockwise moment produced by P , the Moment has to be clockwise to counter the effect , am i right ? Just like the case in post#1 ...

 

[CivilSigma]

How about the case in post#2 ? Why
M = -Pv ? For this case , why the M at the bottom = clockwise? since to balance the anticlockwise moment produced by P , the Moment has to be clockwise to counter the effect , am i right ? Just like the case in post#1 ...

Yes, that's correct. So, note that in post#2 , the assumed direction of the moment in figure (b) is incorrect as it is drawn counter clockwise.

 

[fonseh]

Yes, that's correct. So, note that in post#2 , the assumed direction of the moment in figure (b) is incorrect as it is drawn counter clockwise.

So , in notes 2 , the assumed direction of the moment should be in clockwise direction . So , M = Pv ?
But , i checked out so many books and so may links , they still give M = -Pv , so are they all wrong ?

 

[CivilSigma]

So , in notes 2 , the assumed direction of the moment should be in clockwise direction . So , M = Pv ?
But , i checked out so many books and so may links , they still give M = -Pv , so are they all wrong ?

No , M=-Pv is correct for the assumed internal moments (positive is counter clockwise) as seen in figure (b). The assumed internal moment is counter clockwise in direction and the force P also rotates the column in a counter clockwise motion. So, ΣMoments = 0 , M+Pv=0 , M=-Pv.

Obviously, since the column is assumed to be in equilibrium, the internal moment will actually be clockwise. This is exactly what the equation tells us, M= - Pv, the negative sign means that the assumed internal moment is equal to PV but is clock wise. But the example doesn't explicitly state this. For mathematical consistency we assign clockwise moments a negative sign, and counter clock wise moments a positive sign.

 

[fonseh]

No , M=-Pv is correct for the assumed internal moments (positive is counter clockwise) as seen in figure (b). The assumed internal moment is counter clockwise in direction and the force P also rotates the column in a counter clockwise motion. So, ΣMoments = 0 , M+Pv=0 , M=-Pv.

Obviously, since the column is assumed to be in equilibrium, the internal moment will actually be clockwise. This is exactly what the equation tells us, M= - Pv, the negative sign means that the assumed internal moment is equal to PV but is clock wise. But the example doesn't explicitly state this. For mathematical consistency we assign clockwise moments a negative sign, and counter clock wise moments a positive sign.

Do you mean for all the cases in post 1 and post 2 , the author assumed the internal moment is in counter clockwise direction ?

 

[CivilSigma]

Do you mean for all the cases in post 1 and post 2 , the author assumed the internal moment is in counter clockwise direction ?

Yes, but in case 1 it is not an internal moment but a reaction moment

 

[fonseh]

Do you mean for all the cases in post 1 and post 2 , the author assumed the internal moment is in counter clockwise direction ?

It seems that the theory that the author assumed that the moment is counterclckwise all the time is incorrect here . I have 2 example below (from another book) . We can see that in the firstexample ( photo 1 and photo 2) book , the assumed internal moment is clockwise , for another case(photo 3 and photo4) , we can see that the reaction moment is clockwise

 

[CivilSigma]

You can assume any direction to be positive, but for that particular problem, you need to be consistent and carry out the same assumption.

 

[fonseh]

You can assume any direction to be positive, but for that particular problem, you need to be consistent and carry out the same assumption.

please refer to the edited post in post #12 .

 

[fonseh]

You can assume any direction to be positive, but for that particular problem, you need to be consistent and carry out the same assumption.

It seems that the author of the example in the book that i uploaded doesn't follow the rules , or i missed out something ? can you explain it ?

 

[fonseh]

You can assume any direction to be positive, but for that particular problem, you need to be consistent and carry out the same assumption.

I also found that the assumed internal moment always has the same direction with the applied force moment in both example , is this true ? why we need to make that assumption ?

 

[CivilSigma]

Assuming a direction is all but a perspective for positive and negative, have a read about the conventional sign convention:
https://en.wikipedia.org/wiki/Shear_and_moment_diagram#Convention

Also,

I also found that the assumed internal moment always has the same direction with the applied force moment in both example

This is not true, it depends on the situation of analysis. In post #12, question 4.4, the internal moment is drawn counter clockwise and the force P rotates the column clockwise.

 

[fonseh]

Assuming a direction is all but a perspective for positive and negative, have a read about the conventional sign convention:
https://en.wikipedia.org/wiki/Shear_and_moment_diagram#Convention

Also,

This is not true, it depends on the situation of analysis. In post #12, question 4.4, the internal moment is drawn counter clockwise and the force P rotates the column clockwise.

Well , i agree that in 4.4 the assumed moment is counterclockwise , because the moment will turn the beam in U shape (smile curve) . But , i don't understand why in 4.3 , the assumed moment is clockwise , why not anticlockwise ? Because when the assumed moment is anticlockwise , it will bend the beam in U shape

 

[CivilSigma]

It doesn't really matter what direction you assume the moment is as long as you adopt a consistent general sign convention: Assume that all counter clockwise moments are'+' and all clock wise moments are '-'.

Say in our FBD, we drew the unknown internal moment ( call it 'M') counter clockwise, then taking sum of the moments and using the above statement:
(+M) + (-PV) = 0 , then M=PV. How do we interpret this result? It means that the internal moment is of counter cockwise orientation and of magnitude PV.

Say in our FBD, we drew the unknown internal moment ( call it 'M') clockwise, then taking sum of the moments and using the above statement:
(-M) + (-PV) = 0 , then M=-PV. How do we interpret this result? It means that the internal moment is not of clockwise direction (because our answer is negative) , it is of counter clock wise direction and has magnitude PV.

Have a watch:

 

[fonseh]

So , shouldn,t the assumed moment is anticlockwise at the beam to enable it to have a curve U shape ? Just like the case below

 

[fonseh]

Say in our FBD, we drew the unknown internal moment ( call it 'M') counter clockwise, then taking sum of the moments and using the above statement:
(+M) + (-PV) = 0 , then M=PV. How do we interpret this result? It means that the internal moment is of counter cockwise orientation and of magnitude PV.

You are referring to which case ? photo in 483 or photo in 485 ? I'm confused

 

[fonseh]

It doesn't really matter what direction you assume the moment is as long as you adopt a consistent general sign convention: Assume that all counter clockwise moments are'+' and all clock wise moments are '-'.

Say in our FBD, we drew the unknown internal moment ( call it 'M') counter clockwise, then taking sum of the moments and using the above statement:
(+M) + (-PV) = 0 , then M=PV. How do we interpret this result? It means that the internal moment is of counter cockwise orientation and of magnitude PV.

Say in our FBD, we drew the unknown internal moment ( call it 'M') clockwise, then taking sum of the moments and using the above statement:
(-M) + (-PV) = 0 , then M=-PV. How do we interpret this result? It means that the internal moment is not of clockwise direction (because our answer is negative) , it is of counter clock wise direction and has magnitude PV.

Have a watch:

Ya, i understand hat . But , when i try out M = Py , where EI(d2y.dx2) = Py , i gt different things with the derived equation , why can't i do so ?

 

[PhanthomJay]

The negative sign in the "-Py" term is correct, although when you assume the correct direction of the internal moment for the 'pinned-pinned' case, you end up with "+Py", and get the wrong signage in the differential equation . This paradox has confused me for years. I believe the paradox is resolved when you consider that the internal moment is , when written in terms of the curvature - stiffness relationship where the absolute value of M = EI(d^2y/dx^2), that actually M= - EI(d^2y/dx^2), because the curve is concave with a negative curvature. Unlike the cantilever case in you first post, where M is shown correctly and the curvature is convex or positive.

 

[fonseh]

, because the curve is concave with a negative curvature

How do you know that ? When we view it from different sides , it can be negative and positive curvature , right ?

 

[fonseh]

The negative sign in the "-Py" term is correct, although when you assume the correct direction of the internal moment for the 'pinned-pinned' case, you end up with "+Py", and get the wrong signage in the differential equation . This paradox has confused me for years. I believe the paradox is resolved when you consider that the internal moment is , when written in terms of the curvature - stiffness relationship where the absolute value of M = EI(d^2y/dx^2), that actually M= - EI(d^2y/dx^2), because the curve is concave with a negative curvature. Unlike the cantilever case in you first post, where M is shown correctly and the curvature is convex or positive.

Do you mean the author suume that the right is positive axis ? How about the case where the beam is curve to the left ( the max/min point located at the left) ? if this case , M= Py ?

When we apply the axial forces at the end , the beam can be deflected to both right and to the left , right ? just like the below , but , how do we determine that the beam is deflected to which direction ?

 

[PhanthomJay]

It doesn't matter in which direction the column is laterally deflected left or right. First you can adopt a convention that curvature is negative when the shape is concave with respect to the beam axis facing the beam, thus, for the pinned pinned case, curvature is negative for both left or right displacements . In answer to your question on moment signage when beam is deflected left or right for the pinned pinned case, when it deflects right, the applied eccentric moment is Py counterclockwise, and the internal moment M must be clockwise, thus
(-Py) + M = 0, or M = Py; and when it is deflected left , then the eccentric moment Py is clockwise and the internal moment M must be counterclockwise, thus (+Py) - M = 0, or M = Py, which is the same result, so again, it does not matter, and in both cases since M is - (EI)(d^2y/dx^2) , the the differential equation becomes
(EI)d^2y/dx^2 + Py = 0.

 

[fonseh]

I believe the paradox is resolved when you consider that the internal moment is , when written in terms of the curvature - stiffness relationship where the absolute value of M = EI(d^2y/dx^2), that actually M= - EI(d^2y/dx^2), because the curve is concave with a negative curvature.

why this is not stated in the book ? I have Hibbler and Beer books with me , but it's not stated in it

 

[PhanthomJay]

It is not stated in any source I can find. They all seem to throw the minus sign in there without explanation. I am still unclear why. Further , when you apply a tensile load P instead of a compressive load P, the direction of the internal moment changes, but the result is still the same, M = Py, and you get the same differential equation for the buckling solution, although the column will never buckle under tension load, because the column veil self restore to straight under increasing load, so I am still stuck here. I do remember a lecture on this in college about 50 years ago, but my notes have long since disappeared,

 

[fonseh]

It is not stated in any source I can find. They all seem to throw the minus sign in there without explanation. I am still unclear why. Further , when you apply a tensile load P instead of a compressive load P, the direction of the internal moment changes, but the result is still the same, M = Py, and you get the same differential equation for the buckling solution, although the column will never buckle under tension load, because the column veil self restore to straight under increasing load, so I am still stuck here. I do remember a lecture on this in college about 50 years ago, but my notes have long since disappeared,

Ya， i agreed that the beam doesn't buckle under tension load , IF the beam doesn't buckle , why there is moment Py ?

 

[PhanthomJay]

Ya， i agreed that the beam doesn't buckle under tension load , IF the beam doesn't buckle , why there is moment Py ?

There would still be moment if the column was not ideally straight or if it was displaced laterally, even for the compression case, with lateral displacement or a not straight column, the collimn would not buckle if the applied load was less than the critical load.