Novark
- 14
- 0
[Solved]
KCL, KVL, Ohms Law
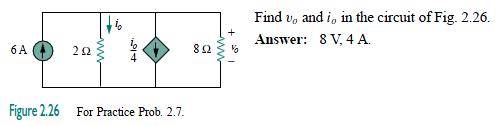
6 = i + (i/4) + (v/8)
I just can't get another equation that relates v & i.
Any suggestions? Am I going about this the right way?
Homework Statement
Homework Equations
KCL, KVL, Ohms Law
The Attempt at a Solution
6 = i + (i/4) + (v/8)
I just can't get another equation that relates v & i.
Any suggestions? Am I going about this the right way?
Last edited: