Simple Moments Question with a Chest of Draws

[xxJaRxx]

Hello,

My friend and I have been having a discussion about moments (when applied to a chest of draws).

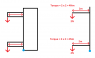
The argument is; if the weight in each draw is the same, and anyone draw is opened fully, will a draw higher up be more likely to cause the chest of draws to tip forwards, or are they all the same? For example, I have the same heavy weight in all draws of my chest of draws, I open the bottom draw fully, it does not tip over so I close it, I then open the top draw... the same thing should happen right and it should not tip? Because in terms of moments, the weight vertically down is exactly the same in both cases and the horizontal distance from the pivot point to end of the draw is also the same in both cases?

Assuming we ignore the force of pulling on the draw, which would add a force in a different direction.

 

[phillip1882]

i think you mean drawers not draws.
i think it depends on the pivot point. if its in the middle, then yes, won't tip over. but if below middle then may or may not tip over.

 

[xxJaRxx]

You are correct, I mean drawers.

Surely the pivot point will always be the same? The pivot point will be the front edge of the chest of drawers, that is on the floor. So when it tips there is a moment around this point. It could be thought of as a 'hinge' like on a door.

Anyone have an answer? I have drawn a pretty picture to convey my opinion and theory behind it.

Summary of the question - does the height of the drawer have any impact on the point where it tips, if all the weight is equal and only one drawer is open at a time?

 

[Studiot]

Hello JaR, welcome to Physics Forums.

I would have thought this question would have attracted more attention in the general physics section, it is after all a physics question, not a maths one.

That said your general approach is sound.

A couple of small points arise though.

The downward force offered by the drawer acts through the centre of gravity of the extended part of the drawer, not at its extremity. For a uniform section drawer this is at its midpoint.

So when it tips there is a moment around this point

An open drawer always exerts a moment about this point. Until tipping this is counterbalanced by the moment of the weight of the chest frame acting through its centre of gravity

 

[xxJaRxx]

Thanks Studiot.. so the drawer exerts a moment around its centre of gravity, not the pivot point of the chest of drawers (indicated by the blue dot)?

Can you possibly answer the question; does the height of the drawer have any impact on when the chest of drawers tips, if all the weight is equal and only one drawer is open at a time?

 

[Studiot]

so the drawer exerts a moment around its centre of gravity, not the pivot point of the chest of drawers

Not exactly. A force always exerts amoment about any point or line that its line of action does not pass through.

There are two ways to attack this question. They lead to equivalent equations.

With regard to the attachment and regards the chest of drawers with one drawer open as a single rigid body. For simplicity assume that it has uniform density.

ABCD represents the frame of the chest.
We are considering tipping about the line AD.

When one drawer (EFILGH) is open it is divided into two parts by the line AD.
These parts are EFGH and FILG.

An empty space IJKL is left behind by the opening of the drawer.

One approach is to note that the whole body (with drawer open) ABCDGHEF will topple if the position of the centre of gravity lies to the left of AD and not otherwise.

So you can calculate the potition of the CofG for the two cases with upper and lower drawers open by dividing the whole into rectangles and calculating the contributions to the centre of gravity.

Alternatively (but equivalently) you can take moments about AD and use the condition that for toppling

W₁ *GH > (W₂*GL + W₃*AB + W₄*JM + W₅*DC)

(I have multiplied by 2 throughout here to remove the factors of a half in the distances)

 

[coolul007]

The chest tips over when the center of mass is moved to the left of the vertical line extended from the "tipping point" The bottom drawer cannot "rotate" the chest through an angle great enough to tip the chest. Therefore it must be a drawer that can rotate enough to move the center of mass to the left of the vertical.