Taulant Sholla
- 96
- 5
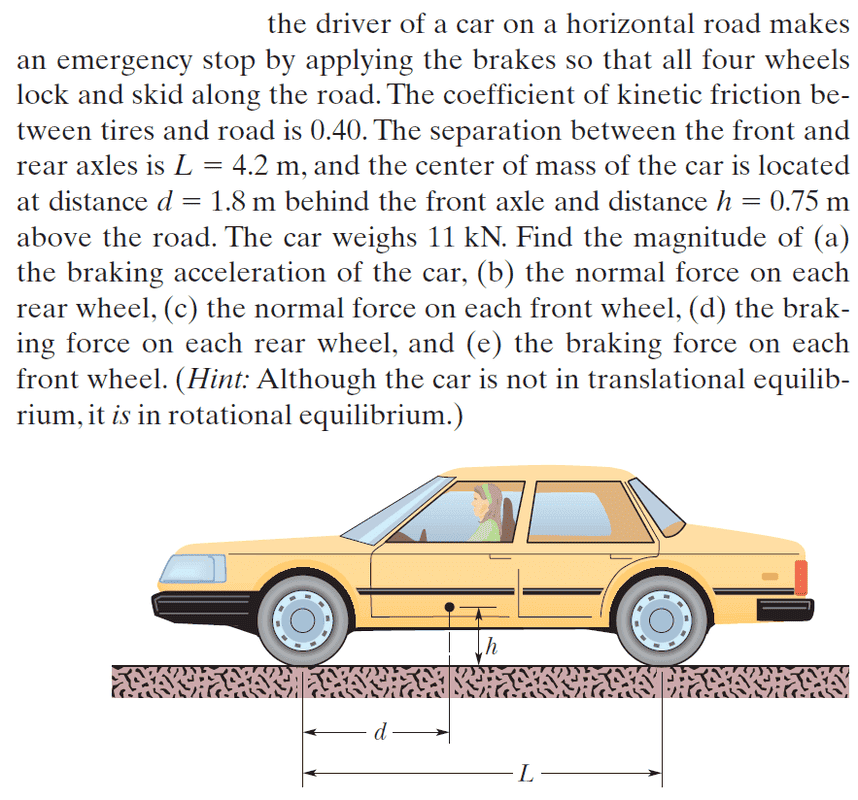
- Homework Statement
- Calculate forces and torques
- Relevant Equations
- Force and torque equilibrium.
I get the correct answer if I use the COM as the axis of rotation for torque calculations. Shouldn't I be able to use any point as the axis of rotation for torque calculations, e.g. where the front wheels make contact with the ground?