Tekneek
- 70
- 0
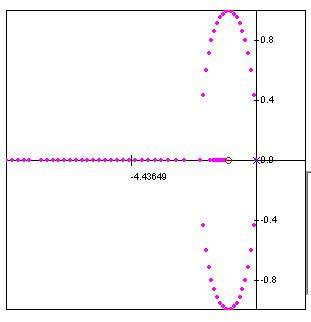
The characteristic equation is 1+K(S+1)/S2 Below is the root locus diagram. I don't get why there are two branches when there is only one pole, at 0. Does it count as having two poles even if it is the same because of s^2 ? If it does then why doesn't the angle of departure make sense?
number of poles(n) = 2
number of zeros(m) = 1
angle = (2h+1)/n-m * 180 = keep getting the same angle, 180
The angle certainly does not look like 180 as it departs from its pole...
number of poles(n) = 2
number of zeros(m) = 1
angle = (2h+1)/n-m * 180 = keep getting the same angle, 180
The angle certainly does not look like 180 as it departs from its pole...