- #1
Lolagoeslala
- 217
- 0
Homework Statement
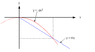
Eddie "The Eagle" Edwards takes off on the 90 m ski-jump with a horizontal velocity of 20 m/s. If the gradient of the landing slope is as shown, find the distance L along the slope covered by his jump,ignore any effect of the air on this eagle.
Image given:
http://s1176.beta.photobucket.com/user/LolaGoesLala/media/yeahok_zps7743bc20.png.html
The Attempt at a Solution
So, they have given us the horizontal velocity which is 20 m/s [ E ]
and i am not sure what the 90 m represent.
Is it the verticle length or is the diameter along the base of the triangle.