r_prieto5
- 18
- 0
Hello everyone,
So for a personal project I want to calculate the force necessary for a solenoid (electromagnetic coil) to keep a permanent magnet triangle locked diagonally up and down at the same time so that it does not move in any direction. I need to know the values for coil thickness, amps, turns, and pretty much anything else necessary. The distance should be around 2 mm separation between faces and the weight of the triangle is around 2 kg. In the sketch, the green things are electromagnets attracting with forces Fsi and Fsii and purple is the triangle with forces Fmi and Fmii, all magnets are horizontally locked by the wall, it is just a vertical movement controlled by the magnets pulling on the triangle. This is not a homework or anything so feel free to give comments, formulas (hopefully with links to source), or any information I could use.
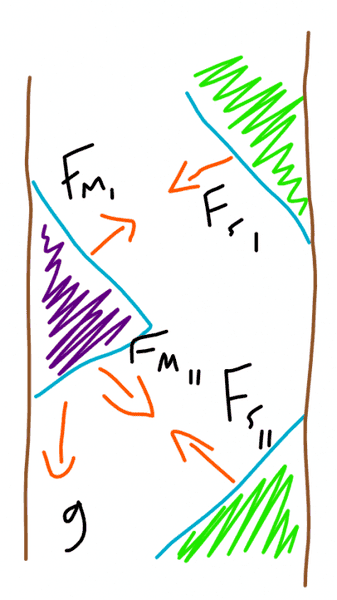
So for a personal project I want to calculate the force necessary for a solenoid (electromagnetic coil) to keep a permanent magnet triangle locked diagonally up and down at the same time so that it does not move in any direction. I need to know the values for coil thickness, amps, turns, and pretty much anything else necessary. The distance should be around 2 mm separation between faces and the weight of the triangle is around 2 kg. In the sketch, the green things are electromagnets attracting with forces Fsi and Fsii and purple is the triangle with forces Fmi and Fmii, all magnets are horizontally locked by the wall, it is just a vertical movement controlled by the magnets pulling on the triangle. This is not a homework or anything so feel free to give comments, formulas (hopefully with links to source), or any information I could use.