Solution to Classical Mechanics Problem: Removing Constant Terms

[rmfw]

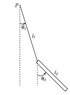
Ayo everybody, I'm doing a problem about theory of small oscilatons (see pic) and I got the following for potential energy:

$V= mg(\frac{l_{2}}{2} +\frac{l_{1}}{2} \theta^{2}_{1} + \frac{l_{2}}{4} \theta^{2}_{2})$ (after the aproximation $cos \theta$~ $1 - \frac{\theta^{2}}{2}$

Knowing that $V = \frac{1}{2} V_{jk} \theta_{jk}$ I need to write the matrix $V_{jk}$

Since the term $mg\frac{l_{2}}{2}$ is constant, can I remove it from the potential ?

And write the matrix like this:

$V_{jk} =mg \begin{pmatrix}<br /> l_{1} & 0 \\<br /> 0 & \frac{l_{2}}{2} \\<br /> \end{pmatrix}$

If not, how can I remove the constant term?

 

[mfb]

Constant terms don't matter, you can ignore them. They just reflect the arbitrary choice of "zero height".