Solve Bernoulli Problem: Mass of Water in Tube

[JulienB]

Homework Statement

Hi everybody! I'm back with another Bernoulli problem :)

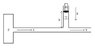
A reservoir with constant pressure P = 10⁵ Pa releases through a tube water (density ρ = 1 g/cm³) with the velocity v = 4 m⋅s^-1. That tube is then connected to another perpendicular tube (area A = 0.1 m², height h = 2m) in which the water doesn't move and holds a mass m covering the whole area.
What is the mass m?

(sorry for the poor problem statement, it's hard to translate from German to English since neither of those languages are my mother language :) see attached picture for a better comprehension).

Homework Equations

Bernoulli equation, pressure, forces.
I also immediately convert ρ into ρ = 1000 Kg/m³.

The Attempt at a Solution

Okay I'm posting that problem here because I feel like I still get confused about how to deal with some inputs in the Bernoulli equation. Here is what I've done:

Since the mass is not moving, I believe ΣF = 0, which means that the force of the water on the mass (F_U) is equal to the force of gravity of the mass on the water:

ΣF = 0 ⇔ mg = F_U

Next step I want to know the pressure (P₁) at the point where the water and the mass meet, and I am a little unsure about my formula:

P₁ = F_U/A = mg/a

Is that correct? I am often unsure what force should be placed in that equation...However I then attempted to substitute that pressure into my Bernoulli equation:

P + ρgh₀ + ½ρv² = P₁ + ρgh + ½ρv₁²

(ρgh₀ = 0 because h₀ = 0, ½ρv₁² = 0 since the water is not moving)

⇔ P + ½ρv² = mg/A + ρgh
⇔ m = (A/g)(P + ½ρv² - ρgh)
⇔ m = 880 Kg

What do you guys think?

Thank you very much in advance for your answers, I appreciate your help.Julien.

 

[Chestermiller]

The pressure in the tank is P (and the velocity inside the tank is zero), but the pressure within the tube is $P-\frac{1}{2}\rho v^2$. This is also the pressure underneath the vertical pipe. The reason that pressure in the tube is less than P is that part of the pressure was used to accelerate the fluid to the tube velocity. Use Bernoulli to determine the pressure directly underneath the vertical pipe, and you will see this. So, in your final equations, there should be a minus sign in front of the $\frac{1}{2}\rho v^2$, rather than a plus sign. Everything else is done correctly.

Chet

 

[JulienB]

@Chestermiller Hi Chet, and thank you for your answer! Indeed I see what you mean with the pressure within the tube, I didn't reflect upon the fact that the water has no velocity inside the tank. But I fail to obtain P - ½ρv² on the left side of my Bernoulli equation, since the - ½ρv² cancels with the + ½ρv² (which also kind of makes sense). I'm sure I am missing something, because the way I've done it makes the information about the velocity in the tube irrelevant.

I get m = 800 kg now. I've attached my equations with the post.

Julien.

 

[Chestermiller]

@Chestermiller Hi Chet, and thank you for your answer! Indeed I see what you mean with the pressure within the tube, I didn't reflect upon the fact that the water has no velocity inside the tank. But I fail to obtain P - ½ρv² on the left side of my Bernoulli equation, since the - ½ρv² cancels with the + ½ρv² (which also kind of makes sense). I'm sure I am missing something, because the way I've done it makes the information about the velocity in the tube irrelevant.

I get m = 800 kg now. I've attached my equations with the post.

Julien.

Bernoulli can't be applied to points 1 and 2 because point 2 is not on a streamline. Between points 1 and 2, you just apply the hydrostatic equilibrium equation. If you didn't know the lower pipe was there (say it was covered), you would conclude that the material in the vertical column would have to satisfy hydrostatic equilibrium.

 

[JulienB]

@Chestermiller Thank you, that was a very clear explanation. I now see how to obtain the - ½⋅ρ⋅v², but I do not have the - ρ⋅g⋅h anymore, which I guess should be there.

 

[JulienB]

(Also, I assumed we are dealing with gauge pressure throughout the whole problem - is that a correct assumption?)

 

[Chestermiller]

(Also, I assumed we are dealing with gauge pressure throughout the whole problem - is that a correct assumption?)

Yes.

 

[JulienB]

@Chestermiller Could it be that the -ρgh is the pressure at the top (point (2))?

ΣF = 0 = P₁⋅A - P₂⋅A - m⋅g
⇔ m⋅g = A⋅(P₀ - ½⋅ρ⋅v² - ρ⋅g⋅h)
⇔ m = 720 kg

 

[Chestermiller]

@Chestermiller Could it be that the -ρgh is the pressure at the top (point (2))?

ΣF = 0 = P₁⋅A - P₂⋅A - m⋅g
⇔ m⋅g = A⋅(P₀ - ½⋅ρ⋅v² - ρ⋅g⋅h)
⇔ m = 720 kg

Your force balance on the piston showed that the pressure at point 2 is mg/A. However, the equations you have written here are correct.

 

[JulienB]

@Chestermiller I think I get it now, thank you once again for your very valuable help!

I attach to this post my final complete answer for other people searching infos on the topic.