Touchme
- 41
- 0
Homework Statement
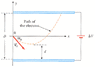
An electron is fired at a speed vo = 5.0 106 m/s and at an angle o = -44° between two parallel conducting plates that are D = 3.7 mm apart, as in Figure P16.66. The voltage difference between the plates is V = 100 V.
(a) Determine how close, d, the electron will get to the bottom plate.
Homework Equations
Conservation of energy:
(1/2)mv^2 = -qEd
E=V/D
The Attempt at a Solution
I was thinking conservation of energy because the electron is initially moving and when it reaches max, it stops and KE is converted to PE.
(1/2)(9.109e-31)[(5e6)sin(44)]^2 = (-1.602e-19)(27027.02)(d)
d = 0.001269 m
E = (100/0.0037) = 27027.2 N/C
Anyone knows what is wrong?
Attachments
Last edited: