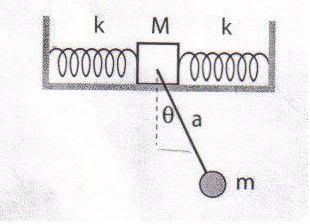
First, notice that there are only two degrees of freedom: 1. The box can move side-to-side (x), and 2. the pendulum can swing about (\theta).
So let us first consider the
kinetic energy of the system. The kinetic energy of the box can trivially be written as
T_\text{box}=\frac{1}{2}M\dot{x}^2.
The kinetic energy of the pendulum is not quite so trivial. We must first write its general position in terms of the cartesian coordinates and then differentiate them with respect to time to yield its velocity.
After a little inspection you should be able to convince yourself that the
x and
y-coordinates of the pendulum at some general time is given by
X=x+a\sin\theta
Y=a\cos\theta.
A time differentiation yields
\dot{X}=\dot{x}+a\dot\theta\cos\theta
\dot{Y}=-a\dot\theta\sin\theta.
We can square each component to find the velocity-square of the pendulum:
\dot{X}^2=\dot{x}^2+a^2\dot\theta^2\cos^2\theta+2a\dot{x}\dot\theta\cos\theta
\dot{Y}^2=a^2\dot\theta^2\sin^2\theta.
v^2=\dot{X}^2+\dot{Y}^2=\dot{x}^2+a^2\dot\theta^2+2a\dot{x}\dot\theta\cos\theta
Therefore, we can write the kinetic energy of the pendulum as
T_\text{pend}=\frac{1}{2}m\left(\dot{x}^2+a^2\dot\theta^2+2a\dot{x}\dot\theta\cos\theta\right).
Now, let's consider the
potential energy of the system. Turn your attention to the springs. If we assume that the spings are streched far beyond their natural lengths, we can ignore it. So we can use Hooke's law to write the potential energies of the two springs:
U_\text{springs}=\frac{1}{2}kx^2+\frac{1}{2}k(-x)^2=kx^2
Finally, we can write the gravitational potential energy of the system. If we define our reference height to be level with the springs, the gravitational potential energy of the box is 0. However, the gravitational potential energy of the pendulum is
U_\text{grav}=mg(\text{height})=-mga\cos\theta.
After combining the appropriate energies derived above, we arrive at the Lagrangian of the system:
L=T-U=\frac{1}{2}M\dot{x}^2+\frac{1}{2}m\left(\dot{x}^2+a^2\dot\theta^2+2a\dot{x}\dot\theta\cos\theta\right)-kx^2+mga\cos\theta