cyberdeathreaper
- 46
- 0
Here's the problem:
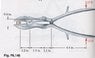
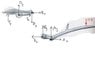
"The bone rongeur shown [refer to attachment] is used in surgical procedures to cut small bones. Determine the magnitude of the forces exerted on the bone at E when two 25-lb forces are applied as shown."
I understand that this "machine" can be broken into 4 free-body diagrams, and then I can use the equilibrium equations on each one to supposedly find the answer. However, my equations don't readily give me a way to solve for the force at E. Any ideas?
Here's all the equilibrium equations I have come up with:
For the top left piece...
<br /> \sum F_x = 0 = D_x + B_x<br />
<br /> \sum F_y = 0 = F_E + D_y - B_y<br />
<br /> \sum M_D = 0 = -1.2 F_E - 1.6 B_y - 0.45 B_x<br />
For the top right piece...
<br /> \sum F_x = 0 = -B_x + A_x<br />
<br /> \sum F_y = 0 = B_y + A_y - 25<br />
<br /> \sum M_A = 0 = -110 -1.1 B_y + 0.45 B_x<br />
It should be obvious that the bottom pieces are symmetric with the top pieces, and similar in their equilibrium equations.
NOTE: The book indicates the answer is 133.3 lb.
"The bone rongeur shown [refer to attachment] is used in surgical procedures to cut small bones. Determine the magnitude of the forces exerted on the bone at E when two 25-lb forces are applied as shown."
I understand that this "machine" can be broken into 4 free-body diagrams, and then I can use the equilibrium equations on each one to supposedly find the answer. However, my equations don't readily give me a way to solve for the force at E. Any ideas?
Here's all the equilibrium equations I have come up with:
For the top left piece...
<br /> \sum F_x = 0 = D_x + B_x<br />
<br /> \sum F_y = 0 = F_E + D_y - B_y<br />
<br /> \sum M_D = 0 = -1.2 F_E - 1.6 B_y - 0.45 B_x<br />
For the top right piece...
<br /> \sum F_x = 0 = -B_x + A_x<br />
<br /> \sum F_y = 0 = B_y + A_y - 25<br />
<br /> \sum M_A = 0 = -110 -1.1 B_y + 0.45 B_x<br />
It should be obvious that the bottom pieces are symmetric with the top pieces, and similar in their equilibrium equations.
NOTE: The book indicates the answer is 133.3 lb.