zorro
- 1,378
- 0
Homework Statement
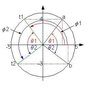
A particle executes simple harmonic motion along a straight line with mean position at x=0, period 20s and amplitude 5cm. The (shortest) time in seconds taken by the particle to got from x=4cm to x=-3cm is?
The Attempt at a Solution
Let the equation be x=Asin(wt+Φ)
At t=0, let x=4 so that sinΦ=4/5
At t=t, putting x=-3 we get wt=sin-1(-3/5) - sin-1(4/5)
Solving for t we get t=-5s
Where is my mistake?