Solve Thevenin Problem: Find Rth & Vth for Points A+B

[Sastronaut]

Homework Statement

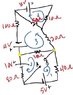
Use thevenin techniques to find the equivalent circuit (Rth and Vth) to which the points A + B are attached.

Homework Equations

Kirchoffs loop rules
V=IR

The Attempt at a Solution

I have indicated my chosen loops in blue. I am not quit sure at this point how to apply kirchhoffs loop rule to each of the loops so that I can determine Vth. the only loop I felt confident on was number 1 i.e. 1: 5V-40ΩI1+Vth. There so much going on in the circuit that its hard from me to determine which way current is flowing so that I can create a junction rule for the wire between the yellow points. Any help would be greatly appreciated!

 

[phinds]

So why not redraw the circuit so that it looks less confusing?

Also, your loops 1 and 2 are useless since they "loop" around open circuits, which are not really loops at all.

 

[Sastronaut]

how do you purpose I re-draw it

 

[phinds]

It was a suggestion. Don't do it if you don't want.

You have not addressed my comment about your loops 1 and 2