- #1
ttiger2k7
- 57
- 0
[SOLVED] Water Refraction
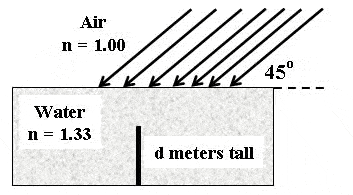
An opaque stick which is d = 1.93 meters tall stands vertically upright on the bottom of a pool of clear water. Parallel rays of sunlight making an angle of 45.0 degrees with the water?s surface illuminate the pool as shown. What is the length of the shadow the stick casts on the bottom of the pool?
n_{a}=1.00
n_{b}=1.33
So I just took
arctan(\frac{1.33}{1.00})=53.06
And I need the angle that will form a triangle with the rod, so
90-53.06=36.94
Then, since the shadow forms the base of a triangle, I solved for it:
tan(36.94)=\frac{opp}{adj}=\frac{opp}{1.93m}
Adn I got that the shadow equals 1.45 m, which was incorrect. What am I doing wrong?
Homework Statement
An opaque stick which is d = 1.93 meters tall stands vertically upright on the bottom of a pool of clear water. Parallel rays of sunlight making an angle of 45.0 degrees with the water?s surface illuminate the pool as shown. What is the length of the shadow the stick casts on the bottom of the pool?
Homework Equations
n_{a}=1.00
n_{b}=1.33
The Attempt at a Solution
So I just took
arctan(\frac{1.33}{1.00})=53.06
And I need the angle that will form a triangle with the rod, so
90-53.06=36.94
Then, since the shadow forms the base of a triangle, I solved for it:
tan(36.94)=\frac{opp}{adj}=\frac{opp}{1.93m}
Adn I got that the shadow equals 1.45 m, which was incorrect. What am I doing wrong?
