Alex126
- 84
- 5
Hi. The problem is really simple I think, but I feel like the text is wrong even though the result seems to be correct.
1. Homework Statement
An object of known mass m (71.5 Kg) is pushed on a [flat] surface with a known friction coefficient of μ (0.272). How much does the object move with a work W (642 J) ?
W = F*s
Friction force = Normal force * μ
The way I solved it, and the result seems to be correct at 3.36 meters, is like this.
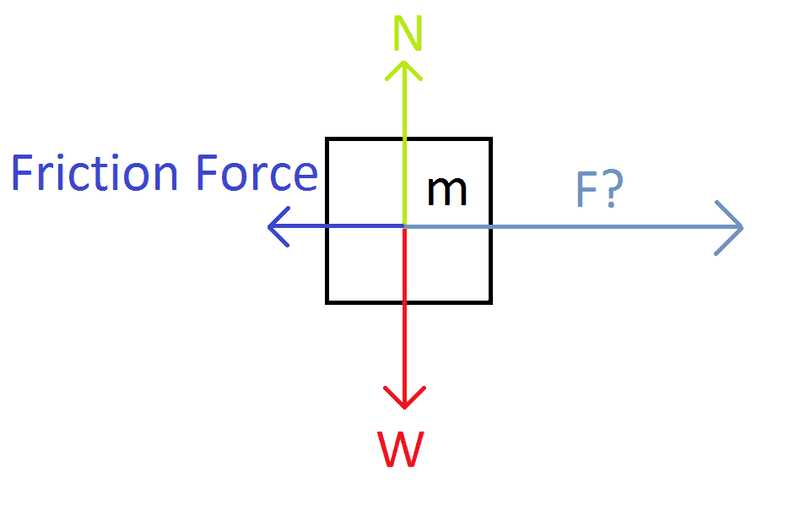
Friction force = m*g*μ (since it's a flat surface, the Normal force = Weight force) = 191 N
W = F*s
642 = 191 * s => s = 642/191 = 3.36
The problem is, I feel like it's missing a piece of the puzzle, and more specifically the Force F that pushes the object in the first place (called F? in the drawing).
What I mean is, the Work should be given by F*s, but "F" here should be the total Forces along the "movement axis" of the object...right? So I thought that the F in W = F*s in this case should have been:
F = -Friction Force + Force_that_pushes_the_object
I figured I'd try solving the exercise assuming that F = Friction Force, and it turns out that the result is in fact correct. However, I feel like saying that the result "matches the result of the workbook" is more accurate than saying that it's "correct", because I really believe that the F should be = Force_push - Friction Force, and not F = Friction Force.
So, in my opinion, the text should have given the additional information on how much F? is worth, and then the solution should have been:
s = Work / (F? - Friction)
Am I wrong?
1. Homework Statement
An object of known mass m (71.5 Kg) is pushed on a [flat] surface with a known friction coefficient of μ (0.272). How much does the object move with a work W (642 J) ?
Homework Equations
W = F*s
Friction force = Normal force * μ
The Attempt at a Solution
The way I solved it, and the result seems to be correct at 3.36 meters, is like this.
Friction force = m*g*μ (since it's a flat surface, the Normal force = Weight force) = 191 N
W = F*s
642 = 191 * s => s = 642/191 = 3.36
The problem is, I feel like it's missing a piece of the puzzle, and more specifically the Force F that pushes the object in the first place (called F? in the drawing).
What I mean is, the Work should be given by F*s, but "F" here should be the total Forces along the "movement axis" of the object...right? So I thought that the F in W = F*s in this case should have been:
F = -Friction Force + Force_that_pushes_the_object
I figured I'd try solving the exercise assuming that F = Friction Force, and it turns out that the result is in fact correct. However, I feel like saying that the result "matches the result of the workbook" is more accurate than saying that it's "correct", because I really believe that the F should be = Force_push - Friction Force, and not F = Friction Force.
So, in my opinion, the text should have given the additional information on how much F? is worth, and then the solution should have been:
s = Work / (F? - Friction)
Am I wrong?