kjlchem
- 23
- 0
Homework Statement
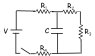
A circuit is constructed with four resistors, one capacitor, one battery and a switch as shown. The values for the resistors are: R1 = R2 = 49 Ω, R3 = 64 Ω and R4 = 64 Ω. The capacitance is C = 88 μF and the battery voltage is V = 24 V.
The switch has been open for a long time when at time t = 0, the switch is closed. What is I1(0), the magnitude of the current through the resistor R1 just after the switch is closed?
Homework Equations
C = Q/V
V=IR
The Attempt at a Solution
Currents in series are the same, so I2=I3. Currents going into a junction = currents coming out so, I1=I4. I think it might all be the same current.
V= I1(R1+R4) + Q/C
Q/C=(R2+R3)I2
I don't know how to find Q/C or I2.