DoobleD
- 259
- 20
Take the following circuit (capacitor initially not charged) :
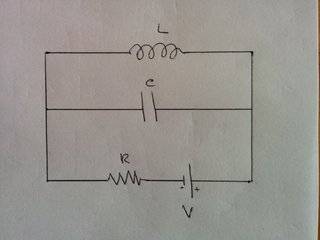
I am trying to solve for the current everywhere as a function of time. I set up the following equations (are they right ?) :
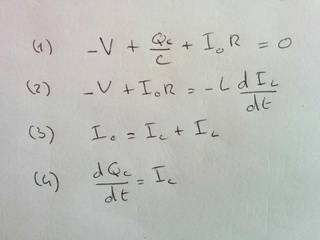
Then, any way I try it, I end up with some messy integrals. Even using wolfram alpha to get those integrals solutions, I can't find out I_0 (current in the bottom wire with the battery), I_C (current in the middle wire with the capacitor), and I_L (current in the upper wire with the inductor) as functions of time.
I suspect it shouldn't be that messy, I must miss something somewhere. Can anyone solve this for me?
I understand that :
- at first (t = 0, battery just plugged) the current must be 0 in the inductor (upper wire) and equal to VR in the middle and lower wires
- after a long time (t = infinity), current must be 0 in the capacitor (middle wire) and equal to VR in the inductor (upper wire) and in the resistance (lower wire)
What I am trying to understand is what happens in between t = 0 and t = infinity.
I am trying to solve for the current everywhere as a function of time. I set up the following equations (are they right ?) :
Then, any way I try it, I end up with some messy integrals. Even using wolfram alpha to get those integrals solutions, I can't find out I_0 (current in the bottom wire with the battery), I_C (current in the middle wire with the capacitor), and I_L (current in the upper wire with the inductor) as functions of time.
I suspect it shouldn't be that messy, I must miss something somewhere. Can anyone solve this for me?
I understand that :
- at first (t = 0, battery just plugged) the current must be 0 in the inductor (upper wire) and equal to VR in the middle and lower wires
- after a long time (t = infinity), current must be 0 in the capacitor (middle wire) and equal to VR in the inductor (upper wire) and in the resistance (lower wire)
What I am trying to understand is what happens in between t = 0 and t = infinity.