Leomusic
- 2
- 0
Hi all,
New to the forums here, but I've got a question for you guys:
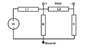
I've ran into this rather peculiar circuit. In all the circuits I've seen (as far as transfer functions go), Vout has always referenced ground (e.g. one node of Vout is ground); in this one, however Vout is across an inductor. I've attached the circuit diagram. (excuse the crudeness of the circuit diagram...quickly whipped it up on Paint ).
).
Find the transfer function Vout(s)/Vi(s) of the circuit.
R=1Ω, L1=2H, L2=3H, C=0.1F
Zr = R; Zl=Ls; Zc=1/Cs; KVL; KCL, etc.
Since Vout wasn't referencing ground, I figured that I needed to use the mesh-current method to get equations for Vi and Vout for each loop. After some rather nasty symbolic matrix algebra, I got expressions for I1 and I2 (loop currents), plugged each of those back into the mesh-current equations, and obtained:
H(s)=\frac{V_{out}}{V_{i}}=\frac{3s^2}{6s^3+5s^2+20s+10}
Is this correct? Also another question: is there a simpler way to do this? Forgive my idiocy but I might be missing something terribly obvious...
It's been a while since this textbook stuff! I tinker around quite a bit with circuits, but I'm no EE...I guess that's what I get for being mechanical
Thanks everyone!
-Leo.
New to the forums here, but I've got a question for you guys:
I've ran into this rather peculiar circuit. In all the circuits I've seen (as far as transfer functions go), Vout has always referenced ground (e.g. one node of Vout is ground); in this one, however Vout is across an inductor. I've attached the circuit diagram. (excuse the crudeness of the circuit diagram...quickly whipped it up on Paint
Homework Statement
Find the transfer function Vout(s)/Vi(s) of the circuit.
R=1Ω, L1=2H, L2=3H, C=0.1F
Homework Equations
Zr = R; Zl=Ls; Zc=1/Cs; KVL; KCL, etc.
The Attempt at a Solution
Since Vout wasn't referencing ground, I figured that I needed to use the mesh-current method to get equations for Vi and Vout for each loop. After some rather nasty symbolic matrix algebra, I got expressions for I1 and I2 (loop currents), plugged each of those back into the mesh-current equations, and obtained:
H(s)=\frac{V_{out}}{V_{i}}=\frac{3s^2}{6s^3+5s^2+20s+10}
Is this correct? Also another question: is there a simpler way to do this? Forgive my idiocy but I might be missing something terribly obvious...
It's been a while since this textbook stuff! I tinker around quite a bit with circuits, but I'm no EE...I guess that's what I get for being mechanical
Thanks everyone!
-Leo.
Attachments
Last edited: