Solving Beam Hinge Torque for Horizontal Force

[NAkid]

Homework Statement

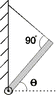
A 35.0kg beam is attached to a wall with a hinge and its far end is supported by a cable. The angle between the beam and the cable is 90o. If the beam is inclined at an angle of theta=14.0o with respect to horizontal, what is the horizontal component of the force exerted by the hinge on the beam? (Use the `to the right' as + for the horizontal direction.)

Homework Equations

The Attempt at a Solution

i know that the horizontal force at pivot must be equal and opposite to horizontal force of tension. so for torques i have
LTsin(theta) = (L/2)mgcos(theta)
Ls cancel
so Tsin(theta) = (1/2)mgcos(theta)

but I don't know what I'm solving for exactly.. when I draw the free body diagram I have that F(horiz)=Fcos(theta), which seems to contradict my equations... help please!

 

[Shooting Star]

LTsin(theta) = (L/2)mgcos(theta)

About which point are you taking the moments?

but I don't know what I'm solving for exactly.. when I draw the free body diagram I have that F(horiz)=Fcos(theta),...

What is F?

First label the forces properly. Resolve into horizontal and vertical components. Without a neat diagram, you will keep making mistakes. Then take the torques about a suitable point.

 

[tiny-tim]

Draw a complete diagram!

Hi NAkid!

Shooting Star is right.

You must draw in the force F at the hinge, and an angle (phi, perhaps?) for it.

And the tension force and the weight force.

It's no good keeping half the diagram in your head - "Without a neat diagram, you will keep making mistakes", and even miss some things completely.

i know that the horizontal force at pivot must be equal and opposite to horizontal force of tension.

Yes, and that's a linear force equation, not a torque, isn't it?

And you haven't written it down, anyway!

so for torques i have
LTsin(theta) = (L/2)mgcos(theta)
Ls cancel
so Tsin(theta) = (1/2)mgcos(theta)

I'm not sure what you've done here.

After you've written the linear force equation, do the torque about the hinge, and that should immediatly give you the value of T.

And then …