DrVirz
- 24
- 0
Hi all,
Having trouble with the following question, trying to work out the FBD and forces. I am fine with working out the max tensile and compressive forces however I can't get that far as the two hinges are throwing me off. As I understand, the moment at the hinges should be 0, is this correct? I think my RDy and RAy are incorrect as I somehow have to incorporate vertical forces at C and B..?
Thanks for your help!
I have attached a photo of the question and my attempted solution for the forces.

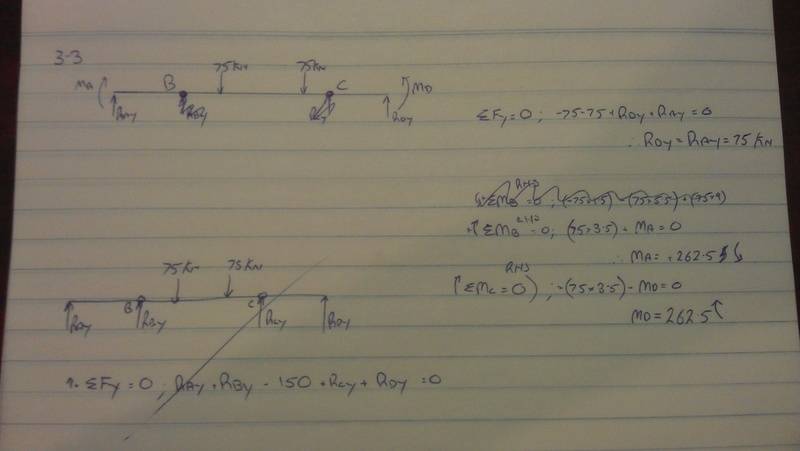
Having trouble with the following question, trying to work out the FBD and forces. I am fine with working out the max tensile and compressive forces however I can't get that far as the two hinges are throwing me off. As I understand, the moment at the hinges should be 0, is this correct? I think my RDy and RAy are incorrect as I somehow have to incorporate vertical forces at C and B..?
Thanks for your help!
I have attached a photo of the question and my attempted solution for the forces.