Solving Charge on Capacitors | C_1, C_2, C_3

[huh]

Homework Statement

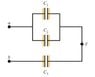
In the circuit shown in the figure, the applied potential is V_ab = 18.0V . For C_1= 3.15(microFarads) , C_2 = 5.50microF , and C_3 = 6.85microF ,

Find the charge q_1 on the capacitor C_1 (and the same for q2 on c2 and q3 on c3)

Picture is attached...

Homework Equations

For capacitors in series: V_total= V_1+V_2+V_3...
= (Q/C)_1+ (Q/C)_2+(Q/C)_3
C_total= Q/V_total 1/C_total= (1/C)_1+(1/C)_2

In parallel: Q= Q_1+Q_2+Q_3=(CV)_1+(CV)_2+(CV)_3

C_total= C_1+C_2+C_3

The Attempt at a Solution

I tried to use Q=CV and got 5.67E-5 or 56.7(w/o changing from microF)...wrong

Then, I tried using the series equation to calculate capacitance, but it didn't work.

I'm confusing myself on how to calculate the stupid charge...

 

[denverdoc]

maybe you're jumping the gun, first what are the voltages across the block, (Vad), and C3 (Vdb)?

 

[quantumdude]

The Attempt at a Solution

I tried to use Q=CV and got 5.67E-5 or 56.7(w/o changing from microF)...wrong

It looks like you just multiplied C_1 by 18V. But the voltage across C_1 is not 18V.

Start by finding the equivalent capacitance. That will allow you to find the total charge on all of the capacitors.

 

[huh]

Would the equivalent capacitance for the whole thing be 6.85E-6

I calculate C1 and C2 together in parallel and then took that answer and did it again with C3.

 

[quantumdude]

That's not what I got. Can you show your steps so we can see what you're doing?

 

[huh]

(1/3.15e-6)+(1/5.5e-6)=4.99278e5

(1/4.99278)= 2.00289e-6

2.00289e-6+ (1/6.85e-6)= 1.45985e5

(1/1.45985e5)= 6.85e-6

 

[quantumdude]

Your mistake is line 1. C_1 and C_2 are in parallel, but you treated them as though they were in series.

 

[huh]

I see what you mean in calculating it as a series. Whoops :)
So would you just add the values for capacitance together?

(3.15e-6)+(5.5e-6)=8.65e-6

8.65e-6+6.85e-6= 1.55e-5

 

[quantumdude]

I see what you mean in calculating it as a series. Whoops :)
So would you just add the values for capacitance together?

(3.15e-6)+(5.5e-6)=8.65e-6

Correct.

8.65e-6+6.85e-6= 1.55e-5

Incorrect. The combination of C_1 and C_2 is in series with C_3. You had that right the first time (although the number you carried over from line 1 was wrong).

 

[huh]

It's in series? It looks like it is in the same position as the first two are...

OK so how do I get it for each individual charge (and capacitance)?

 

[denverdoc]

Capacitors for the purposes of lumping are exactly opposite to resistors: when in parallel they add numerically, and when in parallel, they add as resistors in series. If you think about the latter, it makes sense as one is adding more surface area while keeping the dialectric thicknes constant, ie just making the plates bigger. Now when adding in series, we can't have charge differences under conditions of equilibrium. But those same charges, Q, will lead to different voltages with different capacitances in series. So voltage division around a closed loop will lead to the capacitors sharing voltage unequally. This help at all?

 

[huh]

umm... I'll try reading this again tomorrow... I understand part of what you are saying, but it's not "sticking" in my head right now.
Thanks though...

 

[quantumdude]

It's in series? It looks like it is in the same position as the first two are...

They certainly aren't in the same position. Two circuit elements are in series if they have the same current running through them. They are in parallel if they have the same voltage across them. C_1 and C_2 are obviously in parallel (use KVL to see that), and the combination C_1 and C_2 are obviously in series with C_3. All of the current that flows through the parallel combination, also flows through C_3.

OK so how do I get it for each individual charge (and capacitance)?

Start by analyzing the circuit in which C_1 and C_2 have been reduced to an equivalent capacitance (call it C_{12}). Since that equivalent capacitor is in series with C_3, the two capacitors have to have the same charge. So you should be able to write down a single equation with one unknown: the charge on C_3.