Engineering Solving Circuit for v1, v2, and v3

[VinnyCee]

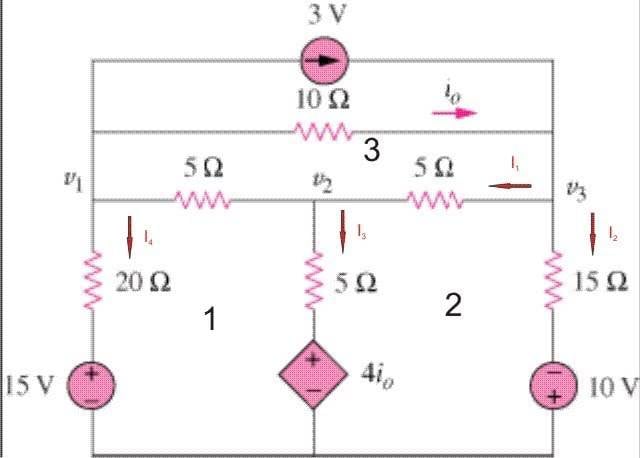
Here is the circuit:

http://img208.imageshack.us/img208/6185/ch3prob26mn0.jpg

We are supposed to find v1, v2 and v3.

My work so far:

i_1\,=\,\frac{v_3\,-\,v_2}{5\,\Omega}\,,\,i_2\,=\,\frac{v_3\,+\,10\,V}{15\,\Omega}\,,\,i_3\,=\,\frac{v_2\,-\,4\,i_0}{20\,\Omega}\,,\,i_4\,=\,\frac{v_1\,-\,15\,V}{20\,\Omega}

(KVL 1): 10\,i_3\,+\,4\,i_0\,=\,5\,i_1\,+\,20\,i_4\,+\,15V

(KVL 2): 15\,i_2\,-\,10\,V\,-\,4\,i_0\,-\,5\,i_3\,-\,5\,i_1\,=\,0

(KVL 3): 5\,i_1\,+\,5\,(i_1\,-\,i_3)\,+\,10\,i_o\,=\,0

(KVL 4 - Loops 1 and 2): 15\,i_2\,-\,10\,V\,-\,15\,V\,-\,20\,i_4\,-\,5\,(i_1\,-\,i_3)\,-\,5\,i_1\,=\,0

Using these equations, I get infinite answers. I did not list KVL 5, which is the whole outer loop, but I think that it is incorrect anyways becuase I am getting 0 = 0 for the last two rows in the matrix. Can someone please help?

EDIT: The 3V source at the top of the schematic should actually be a 3A independent current source.

 

[VinnyCee]

Just checking, but can everyone see the picture with the circuit schematic?

 

[jpr0]

I can't see the schematic. You're trying calculate what the i_n are in terms of the constants 10V, 15V etc?

--I can see it nowYou need one more equation to solve this set, you have 5 unknowns and only 4 equations (unless i_0 is given?)

 

[VinnyCee]

i_0 is not given. What would you suggest as the 5th equation? A supernode, but where?

Do the first four equations look right?

 

[Corneo]

Do you see that i_0 = \frac {v_1-v_3}{10}

BTW I think solving this using KCL is much easier than what you are trying. You only need 3 equations.

 

[doodle]

I agree with Corneo. Since you wanted to solve for the nodal voltages, then nodal analysis (which is KCL) should be more accomodating than mesh analysis (or KVL, which is what you are using now). And like Corneo says, nodal analysis would only give you three equations which appears more reasonable for a exercise of this kind.

But if you should insist on using KVLs, then please check that I3 = (V2 - 4*I0)/20 is incorrect.

 

[VinnyCee]

Where would the three KCL's be applied at? Can you show please?

 

[doodle]

I'll show you one and you try to obtain the rest.

The KCL on node 1 (which has the nodal voltage V1) gives
(V1 - 15)/20 + (V1 - V2)/5 + (V1 - V3)/10 + 3 = 0
or
(7/20) V1 - (1/5) V2 - (1/10) V3 = -9/4
and this becomes Equation #1.

Try to generate the other two KCLs with respect to nodes 2 and 3.

 

[VinnyCee]

Yes, I see that when KCL is applied to a v_n node, that the terms that are not constant in the resulting equation all begin with v_n.

KCL @ v_2:

\frac{v_2\,-\,v_1}{5}\,+\,\frac{v_2\,-\,4\,i_o}{5}\,+\frac{v_2\,-\,v_3}{5}\,=\,0

KCL @ v_3:

\frac{v_3\,-\,v_1}{10}\,+\,\frac{v_3\,-\,v_2}{5}\,+\,\frac{v_3\,+\,10}{15}\,+\,3\,=\,0

Is that correct?

 

[doodle]

KCL @ v_3:

\frac{v_3\,-\,v_1}{10}\,+\,\frac{v_3\,-\,v_2}{5}\,+\,\frac{v_3\,+\,10}{15}\,+\,3\,=\,0

The last equation should read...
\frac{v_3\,-\,v_1}{10}\,+\,\frac{v_3\,-\,v_2}{5}\,+\,\frac{v_3\,+\,10}{15}\,-\,3\,=\,0
since we are summing up the currents leaving the node.

Noting next that I0 = (V1 - V3)/10, the KCL for node 2 can then be written in terms of the nodal voltages only. You will then have 3 unknowns and 3 equations which then becomes a mathematical exercise.

 

[VinnyCee]

RREF\,\left( \begin{array}{cccc}<br /> \frac{7}{20} &amp; -\,\frac{1}{5} &amp; -\,\frac{1}{10} &amp; -\,\frac{9}{4} \\<br /> -\,\frac{11}{20} &amp; \frac{3}{5} &amp; -\,\frac{9}{50} &amp; 0 \\<br /> -\,\frac{1}{10} &amp; -\,\frac{1}{5} &amp; \frac{11}{30} &amp; \frac{7}{3}<br /> \end{array} \right)\,=\,\left( \begin{array}{cccc}<br /> 1 &amp; 0 &amp; 0 &amp; -5.544 \\<br /> 0 &amp; 1 &amp; 0 &amp; -0.691 \\<br /> 0 &amp; 0 &amp; 1 &amp; 4.475<br /> \end{array} \right)

v_1\,=\,-5.544\,V
v_2\,=\,-0.691\,V
v_3\,=\,4.475

Does it look right?

 

[doodle]

\left( \begin{array}{cccc}<br /> \frac{7}{20} &amp; -\,\frac{1}{5} &amp; -\,\frac{1}{10} &amp; -\,\frac{9}{4} \\<br /> -\,\frac{11}{20} &amp; \frac{3}{5} &amp; -\,\frac{9}{50} &amp; 0 \\<br /> -\,\frac{1}{10} &amp; -\,\frac{1}{5} &amp; \frac{11}{30} &amp; \frac{7}{3}<br /> \end{array} \right)\end{array} \right)

I am not sure if the second row is correct. You might want to check.

 

[VinnyCee]

Double checking KCL @ v_2:

\frac{3}{5}\,v_2\,-\,\frac{1}{5}\,v_1\,-\,\frac{4}{5}\,\left(\frac{v_1\,-\,v_3}{10}\right)\,-\,\frac{1}{5}\,v_3\,=\,0

RREF\,<br /> \left(<br /> \begin{array}{cccc} <br /> 0.35 &amp; -0.2 &amp; -0.1 &amp; -2.25 \\<br /> -0.28 &amp; 0.6 &amp; -0.12 &amp; 0 \\<br /> -0.1 &amp; -0.2 &amp; 0.367 &amp; 2.34<br /> \end{array} \right)\,=\,\left( \begin{array}{cccc} 1 &amp; 0 &amp; 0 &amp; -7.178 \\0 &amp; 1 &amp; 0 &amp; -2.767 \\0 &amp; 0 &amp; 1 &amp; 2.912\end{array} \right)

Does this mean that v_1\,=\,-7.18\,V,\,v_2\,=\,-2.77\,V,\,v_3\,=\,2.91\,V?

 

[doodle]

Yup, that looks good to me.