Current Through a Capacitor in a RC Circuit

[Drakkith]

Homework Statement

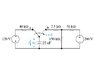
Find $i(0^+)$ and $i(t), t≥0^+$

Homework Equations

The Attempt at a Solution

[/B]
I'm having trouble finding the current through this capacitor. I tried using a KVL loop for $t=0^+$, but I'm doing it incorrectly or something.

Earlier in the problem I found: $v_c(0^+) = -120 V$
Sign convention for resistors: Positive on the top for the 150k resistor, positive on the right side for the other 2.

KVL1: Starting at node $b$ and moving clockwise with current $i_1$ :
$-2.5ki_1+150k(i_1-i_2)-v_c=0$
$-2.5ki_1+150ki_1-150ki_2-(-120)=0$
$147.5ki_1-150ki_2=-120$

KVL2: Starting just to the left of the 50k resistor and moving clockwise:
$-50ki_2+200-150k(i_2-i_1)=0$
$-50ki_2-150ki_2+150ki_1=-200$
$150ki_1-200ki_2=-200$

Solving, I get:
$i_1=0.85 mA$
$i_2=1.6mA$

$i=-i_1=-0.85 mA$

However, this is appears to be incorrect.

 

[berkeman]

Earlier in the problem I found: vc(0+)=−120V

Looks correct.

I tried using a KVL loop

For me, the KVL equations are generally less intuitive and move complicated. Not to make extra work for you, but can you write the KCL equation for the main node in the circuit for t>0 and see if that makes it easier to solve?

 

[Drakkith]

For me, the KVL equations are generally less intuitive and move complicated. Not to make extra work for you, but can you write the KCL equation for the main node in the circuit for t>0 and see if that makes it easier to solve?

Sure. From the main node, $i$ goes left, $i_1$ goes down, and $i_2$ goes right.
$i+i_1+i_2=0$
$\frac{v-v_c}{2.5}+\frac{v}{150k}+\frac{v-200}{50k}=0$
Multiplying both sides by 150k:
$60v-60v_c+v+3v-600=0$
$64v-60(-120)=600$
$64v+7200=600$
$64v=-6600$
$v=-103.125 V$

$i=\frac{v-v_c}{2500}=6.75 mA$
Which is correct...

$i(t)$ is then: $i(t)=6.75e^{(1000t)} mA$

Why in the world did one method work but not the other?

 

[berkeman]

Which is correct...

Yahoo!

Why in the world did one method work but not the other?

Both methods should work, but at least for me, the KVL equations are much less intuitive and therefore much easier to make a mistake when using them. I'll leave it to other (smarter) members (EDIT -- like vela) to find the small typo in your work with the KVL equations...

 

[vela]

Looks like the signs aren't consistent in your KVL equations. If you're going clockwise around the left loop, for example, you should get
$$-2500i_1 + 150000(i_2-i_1) + v_c = 0.$$ In the second KVL equation, the sign on 200 should be negative since you're moving from higher potential to lower potential as you go clockwise around the loop.

 

[Drakkith]

Looks like the signs aren't consistent in your KVL equations. If you're going clockwise around the left loop, for example, you should get
$$-2500i_1 + 150000(i_2-i_1) + v_c = 0.$$ In the second KVL equation, the sign on 200 should be negative since you're moving from higher potential to lower potential as you go clockwise around the loop.

Isn't that already consistent though? Moving from positive to negative voltage across a resistor (moving from higher to lower potential), the sign is +, whereas it's - when moving from negative to positive (as in the $-2500i_1$).

 

[vela]

Isn't what already consistent?

Which way are you assuming the currents $i_1$ and $i_2$ flow? If it's clockwise around the loops, then according to your sign convention, the first term should be $+2500i_1$.

 

[Drakkith]

Isn't what already consistent?

The way I was doing it already.

Which way are you assuming the currents $i_1$ and $i_2$ flow? If it's clockwise around the loops, then according to your sign convention, the first term should be $+2500i_1$.

How so? The negative terminal of the 2500 ohm resistor is on the left.

 

[vela]

Potential drops as the current flows through the resistor. If the current enters on the left, the left end of the resistor is at a higher potential than the right end.

 

[Drakkith]

Looking back at my homework, I can't reconcile what I did there with what I've done here or what you're telling me vela. I'll have to dig a bit deeper and maybe talk to my instructor to figure out what's going on. Thanks all.