Solving Complex Circuits: Need Help With Current Direction

[p75213]

Homework Statement

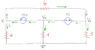
Refer Attachment

Homework Equations

The Attempt at a Solution

I have drawn the current direction in green. Are there any rules regarding the direction of the current?
I am at a bit of a loss regarding the horizontal current through the middle. The best I could come up with is: (V1-V3)/6-V3/3 that is through the 5i voltage source and (V1-V3)/6-V3/3-V2/4 through the 10V voltage source.
For the 10V supernode I have the following equation from KCL: 6V1+6V2+4V3=0. KVL: V1=10+v2.
For the 5i supernode I have the following equation from KVL:V3-V2-5i=0 and i=V1/2.
Therefore V3-V2-5V1/2=0.
Using these equations I get V1=3.85V, V2=-6.15V and V3=3.45V.

Any help would be appreciated.

 

[The Electrician]

The equations you have attributed to KVL: V1=10+v2
and: KVL:V3-V2-5i=0

aren't really KVL equations. KVL says that the sum of the voltages around a closed loop add up to zero. You didn't traverse a closed loop to get those equations. You need those equations, but they are constraint equations rather than KVL equations.

You should probably just treat the 3 nodes (V1, V2 and V3) as a single supernode rather than as two separate supernodes.

You already have 2 equations (the two constraint equations) and you need a third. The currents from the 3 nodes to ground must add to zero, so you just need to form a node equation for the supernode using KCL: V1/2 + V2/4 + V3/3 = 0

Notice that you don't need to form an equation involving the upper 6 ohm resistor; the voltages at the three nodes are completely independent of that resistor (because it's connected across a couple of voltage sources which are in series). However, once you have the node voltages you can calculate the current in the top 6 ohm resistor.

 

[p75213]

Thanks for that Electrician. Joining the two voltage sources into a super duper node makes things much easier.