Solving for Acceleration & Tension: Newton's Laws

[sweet_girl123]

Homework Statement

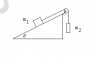
1. For the system shown below use Newton’s Laws to clearly derive an expression for the
acceleration of each mass and the tensions in the cord. The coefficient of friction
between m1 and the incline is 0.100. The mass m1 is 3.00 kg, m2 = 8.00 kg, and θ = 35.0°.
The pulley is frictionless solid disk of mass 0.250 kg.


2. For the system shown below use only Conservation of Energy to clearly derive an
expression for the speed and acceleration of each mass after m2 falls a distance of
2.50 m. The coefficient of friction between m1 and the incline is 0.100. The mass m1 is
3.00 kg, m2 = 8.00 kg, and θ = 35.0°. The pulley is frictionless solid disk of mass
0.250 k

Homework Equations

The Attempt at a Solution

ƩF(x) = m a1

T1 - F - mgSinθ = m1 * a
T2 + m2g = m1a

ƩTorque = IAlpha
-RT1 + RT2 = IAlpha
R(T2-T1) = I (alpha/R)

This is not my homework. This was given to use for practicing for our finals.
Any help would be really helpful
Thank You\

 

[Redbelly98]

You have made a decent start to solving the problem. I have a few comments:

The Attempt at a Solution

ƩF(x) = m a1

T1 - F - mgSinθ = m1 * a

Good, but it looks like you mean to say m1 and not just m on the left side?
You can also look at ƩF(y), that will help you get the friction force F in terms of other quantities.

T2 + m2g = m1a

Think about the direction each force acts, and whether a + or - sign should be in front of each force. Also, I think you mean m₂a on the right?

ƩTorque = IAlpha
-RT1 + RT2 = IAlpha
R(T2-T1) = I (alpha/R)

Why did you replace "Alpha" with "Alpha/r"? I think you meant something slightly different... otherwise this looks good.

This is not my homework. This was given to use for practicing for our finals.
Any help would be really helpful
Thank You\

That's okay, we pretty much like to see people show an attempt at solving the problem, which you did, even when it's not an assignment.

Final comment: I think to solve this they need to tell you what R is for the pulley -- or maybe they tell you what I is. Can you check the problem statement again, and see if I or R for the pulley is given?

Hope that helps.

 

[sweet_girl123]

no there is no R or I is given and only the mass of the pulley is given which is making me confuse. and the part 2 of the quest with the conservation of the energy, I really do not have any idea about that how we do that can you please help me out with that??...:)

 

[JHamm]

If the pulley is frictionless then it won't rotate so it's only function is to redirect the forces, in that case the I and R don't matter and you can essentially forget it is there.

 

[sweet_girl123]

ohhhkk thanks...and for the conservation energy is

1/2m1v^2 + 1/2 M2 V^2 = M1g h sin(X) - (mu)M2g hcos(X)- M2gh
??