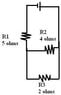
Solving for Current in a Circuit: R1 and R2 Example

[nobb]

Please refer to the attachment. If R1 has a current of 9 A, what is the current through R2? Could someone please explain how to solve this? Thanks.

 

[dextercioby]

Do u know how to apply Ohm's laws...?On a second thought,u need to know what parallel arrangement of resistors is...

Do you have enough clues...?Post the equations.

Daniel.

 

[nobb]

Yes I know how voltage, current, and resistance change in a parallel or series circuit. I am not sure how to start solving this circuit...

 

[dextercioby]

How about applying Kirchhoff's first law for the knot () and the second for the loop with 2 resistors...?

Daniel.

 

[Ouabache]

Yes I know how voltage, current, and resistance change in a parallel or series circuit. I am not sure how to start solving this circuit...

Just start anywhere. If you happen to go off track, we'll lead you back on.

I found the solution with 3 equations, two applying Kirchoff's voltage law, and one using Kirchoff's current law.

 

[scholzie]

Just start anywhere. If you happen to go off track, we'll lead you back on.

I found the solution with 3 equations, two applying Kirchoff's voltage law, and one using Kirchoff's current law.

You can also do it in 1 equation using the current divider rule, if you've learned that.

You know that there are 9 Amps going into the parallel circuit. The current law tells you that \sum I_{in} = \sum I_{out}. You also know that more current flows when there's less resistance. The current divider rule says that, for a simple situation like this, the current through each resistor is the ratio of the "other" resistances to the total resistance times the input current. I don't want to outright give you the answer, but the idea is something like this:

I\ (the\ one\ you\ want\ to\ know) = \frac{(R_{other}) \cdot (I_{input})}{\sum Resistance}

In your situation, you are trying to find I[2], and you know the resistance of R3, you know the input current (9 Amps), so you can use the equation above to get it.

Likewise, if you aren't familiar with that, it's plain to figure it out if you just analize all of the pieces. You know the resistances, so you can find the total resistance using series-parallel equations. You know the current, so you can find the voltage of the power source. Since you know R1 and I1, you can find the voltage drop across R1, and you'll know how many volts are "left over" to be eaten up by the R2/R3 parallel circuit. After that, Ohm's law takes over, and you can find the current in either R2 or R3.

With problems like these it's easy to get confused. The best way to tackle them is to sit and think about all the things you know, find all of the things you can find easily, and then work from there. In this case, everything is given to you and it's easy to start off on the easy things and work towards and answer.


(wow, that was a lot...I didn't expect to write that much! I hope it helped, though)

 

[Doc Al]

I am not sure how to start solving this circuit...

Realize that the voltage across R2 and R3 must be equal. And the total current through both must add to 9A.

 

[Corneo]

Try redrawing the circuit such that you clearly see that R2 and R3 are in parallel. Find the equivalent resistance for the circuit. Find the EMF. Now find the voltage drop across the equivalent resistor consisting of R2 and R3 in parallel. Use the face that R2 and R3 have the same potential, this is the same potential as the one equivalent resistor of R2 and R3. Apply Ohm's Law and your answer should appear.