- #1
nhrock3
- 415
- 0
after we put I2=0 in equations 1 to 3
we have expressions of I1
how did they get I1
because they presented numbers
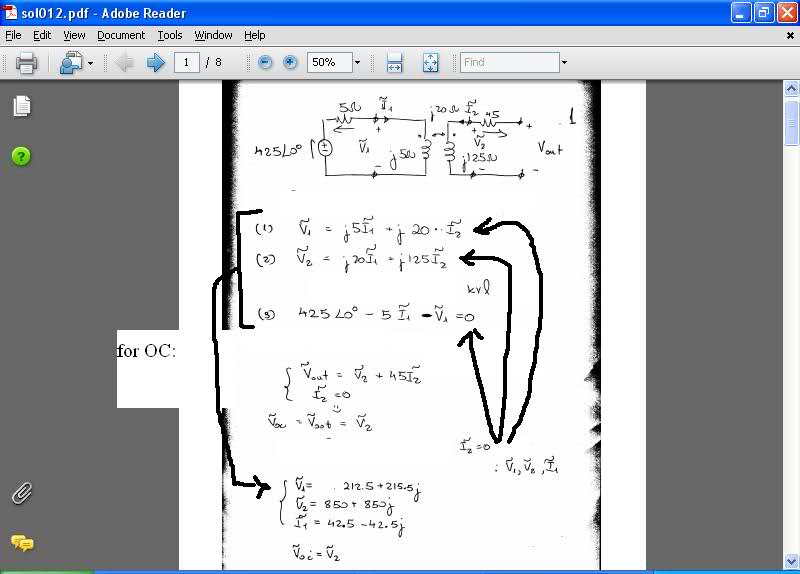
we have expressions of I1
how did they get I1
because they presented numbers
To solve for I1 when I2 is equal to 0, you can substitute I2=0 into equations 1-3. This will eliminate I2 from the equations, allowing you to solve for I1 using basic algebraic methods.
Yes, you can still solve for I1 if I2 is not equal to 0. In this case, you will need to use all three equations (equations 1-3) and solve for I1 using simultaneous equations. This means solving for I1 in one equation, then substituting that value into the other equations until you have a single value for I1.
The possible values for I1 will depend on the specific equations and values given. In general, there can be multiple solutions for I1, or there may be no solution at all. It is important to carefully check your work and make sure your solution makes sense in the context of the problem.
Yes, you can use a calculator or computer program to solve for I1. Many scientific calculators have functions for solving simultaneous equations, and there are also computer programs and online tools that can help you solve for I1 given a set of equations.
Solving for I1 from equations 1-3 with I2=0 can be useful in many scientific and mathematical applications. It allows you to isolate and solve for one variable in a system of equations, which can be applied to a wide range of problems in fields such as physics, engineering, and economics.