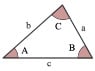
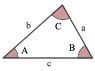
Mark44 said:
Obviously, this isn't right. Please show your work leading up to this value. I suspect that you made a mistake in squaring ##1 + \sqrt 3##
I squared 1+sqrt(3) as (1+sqrt(3))^2=(1+2sqrt(3)+3) =4+2sqrt(3)
For context, this was on my test. Was wondering if someone could solve this from scratch.
So
plugging everything in
b^2= (4+2sqrt(3))+4-(2(1+sqrt(3))(2)Cos(pi/3)
add 4+4+2sqrt(3)=8+2sqrt(3), and finish the"-2acCos(pi/3)" part
b^2=(8+2sqrt(3))-(2+2sqrt(3)(2)(1/2)
(2)(1/2)=1 so cancel that. simplify..
b^2=6
b=sqrt(6)
Lol ok. I messed up my negatives. This is one of many different forms of answers I got. I also tried factoring the hole thing in many different ways during the test and pluging it into the Sine law, but it was very hard to arcsin these. I do not know how to do arcsin(a+b) It was not in any lecture. And then for angle C starting to stack arcsines was starting to seem a bit ridiculous for some reason.
Now, how to find A without a calculator?
Sin(A)/a=Sin(B)/b
Sin(A)/(1+sqrt(3))=Sin(pi/3)/b
Sin(A)=(1+sqrt(3))((sqrt(3)/2))/sqrt(6))
Sin(A)=(1+sqrt(3))(sqrt(3)/2sqrt(6))
Sin(A)=(1+sqrt(3))(1/2sqrt(2))
So I know 1/sqrt(2)=Sqrt(2)/2 .Anyways, this is what I was thinking on the test and was like dammit...
Sin(A)=((1/2sqrt(2))+(sqrt(3)/2sqrt(2))
Sin(A)= (1+sqrt(3))/2sqrt(2)
So how do I arcsine[(1+sqrt(3))/2sqrt(2)] on paper without a calculator? Maybe try to move things around?
arcsin[1/2sqrt(2)+1/2sqrt(3/2)] errm? What? Can I even simplify this way?