Solving Hanging Sign Problem: Find Tension, Horizontal & Vertical Force

  • Thread starter strugglin-physics
  • Start date
  • Tags
    Sign
In summary, the conversation discusses finding the tension in a guy wire connected to a shop sign supported by a uniform beam. The horizontal and vertical forces exerted by the hinge on the beam are also being calculated. However, there is confusion about the equations used to find the tension and the incorrect use of units.
  • #1
strugglin-physics
47
0
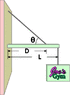
A shop sign weighing 206 N is supported by a uniform 132 N beam of length L = 1.89 m as shown in figure below.

The guy wire is connected D = 1.19 m from the backboard. Find the tension in the guy wire. Assume theta = 43.0 o
Find the horizontal force exerted by the hinge on the beam.
Find the vertical force exerted by the hinge on the beam. Use "up" as the positive direction.

I get T = -mg * 1/2L + T*L*sin(43) = T = mg/2sin(40)

Fx = Hx -T cos(43) = 0
Hx = T cos(43)
Fy = Hy -mg + Tsin(43) = 0
Hy = mg - Tsin(43)

But these are incorrect. Where did I go wrong?
 

Attachments

  • gian0959.gif
    gian0959.gif
    5.5 KB · Views: 695
Physics news on Phys.org
  • #2
"I get T = -mg * 1/2L + T*L*sin(43) = T = mg/2sin(40)"

This is complete nonsense!

You have 3 forces creating torques about the hinge. Which, and where do they act?
 
  • #3
That wasn't suppose to be torque but rather tension.
 
  • #4
It's still nonsense, since your units don't match (T and TL have not the same units)
 

Related to Solving Hanging Sign Problem: Find Tension, Horizontal & Vertical Force

1. What is the hanging sign problem?

The hanging sign problem is a physics problem that involves determining the tension, horizontal force, and vertical force acting on a hanging sign that is attached to two points. It requires applying principles of static equilibrium to find the unknown forces.

2. What are the steps for solving the hanging sign problem?

The steps for solving the hanging sign problem are as follows:
1. Draw a free body diagram of the hanging sign, including all the known and unknown forces.
2. Apply the equations of static equilibrium, which state that the sum of all forces in the horizontal direction and the sum of all forces in the vertical direction must equal zero.
3. Solve for the unknown forces using algebraic equations and substitution.
4. Check your solution by plugging the values back into the equations to ensure that they satisfy the conditions of static equilibrium.
5. If the solution is correct, label the forces on the free body diagram and state the final answer.

3. What are the key principles involved in solving the hanging sign problem?

The key principles involved in solving the hanging sign problem are:
1. Newton's First Law: An object will remain at rest or in motion with a constant velocity unless acted upon by an external force.
2. Newton's Second Law: The net force acting on an object is equal to its mass multiplied by its acceleration.
3. Newton's Third Law: For every action, there is an equal and opposite reaction.
4. Equilibrium: When the net force and net torque acting on an object are both zero, the object is in a state of static equilibrium.

4. What are some common mistakes made when solving the hanging sign problem?

Some common mistakes made when solving the hanging sign problem include:
1. Not drawing a complete and accurate free body diagram.
2. Not correctly setting up and applying the equations of static equilibrium.
3. Incorrectly solving for the unknown forces, such as using the wrong algebraic equations or not considering all the variables.
4. Not checking the solution for accuracy and consistency with the principles of static equilibrium.

5. What are some real-world applications of the hanging sign problem?

The hanging sign problem has many real-world applications, including:
1. Construction: Determining the forces acting on a crane or scaffolding system used for building projects.
2. Architecture: Calculating the forces on a suspension bridge or a cantilevered structure.
3. Physics: Understanding the forces involved in a simple pendulum or a pulley system.
4. Advertising: Designing and installing hanging signs or banners for businesses and events.

Similar threads

Does distance affect torque in hanging sign problem?
    • Introductory Physics Homework Help
2
Replies
42
Views
2K
Force Acting on Hinge: 2744 N Torque on Beam Homework: Find Force on Hinge
    • Introductory Physics Homework Help
Replies
6
Views
1K
How Do You Calculate Forces and Balance a Hanging Cafe Sign?
    • Introductory Physics Homework Help
Replies
18
Views
2K
How Is the Vertical Force Calculated at the Hinge in a Beam and Sign System?
    • Introductory Physics Homework Help
Replies
8
Views
5K
Find the tension in the two strings
    • Introductory Physics Homework Help
Replies
7
Views
1K
Tension and net torque in a cable
    • Introductory Physics Homework Help
Replies
10
Views
4K
Torque for a hanging sign. Finding Tension
    • Introductory Physics Homework Help
Replies
2
Views
10K
Work done on a conical pendulum
    • Introductory Physics Homework Help
Replies
3
Views
1K
Finding tension in string in vertical circle
    • Introductory Physics Homework Help
Replies
1
Views
1K
Vertical circle in a pendulum ride -- tension force acting on the gondola
    • Introductory Physics Homework Help
Replies
7
Views
2K

Hot Threads

Recent Insights

Back
Top