orangeincup
- 121
- 0
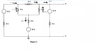
Homework Statement
Determine the voltage across all elements
Homework Equations
i=v/r
v1+v2+v3+..=0
The Attempt at a Solution
I'm not sure which of the nodes I should use to take my KVL from. The a and b are labeled, but should I combine the set of 2-6-6 resistors and label that as an essential node? Should I have four essential nodes?