Solving Moments of Force: Finding A & B

[isigne]

1.

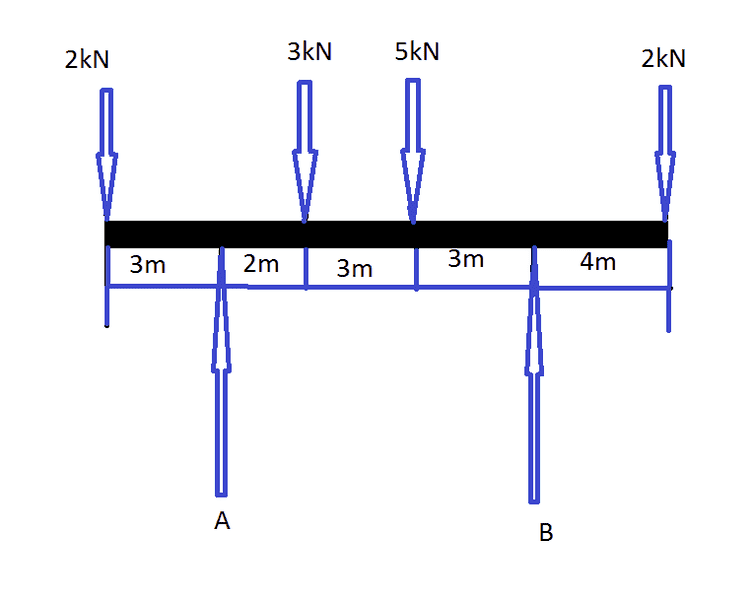
How do I find the force of A and B. I am taking moments at A but I am not getting the correct answer. (More Details below of attempt)

Homework Equations

Ʃ Of Clockwise Moments = Ʃ Of Anti-Clockwise Moments
Ʃ Of Upward Force = Ʃ Of Downward Force

The Attempt at a Solution

(THIS IS WRONG BUT THIS IS MY ATTEMPT)

A => (3x2)+(5x5)+(12x2)= Bx11
=> 6 + 25 + 24 = B x 11
=> 55 = B x 11
=> 55/11 = B
=> 5 = bTHANKS FOR HELP, I was trying this weekend and I need some genius advice so when I get this question again, I will be able to do so :)

 

[Doc Al]

A => (3x2)+(5x5)+(12x2)= Bx11

I assume you're using A as your pivot point.
(1) You neglected the moment due to the 2kN force at the left end.
(2) What's the distance between B and A?

 

[isigne]

This is the link

http://gyazo.com/bcb2e14d67b70ed7b51d9eab837ab547.png