eliassiguenza
- 24
- 0
Homework Statement
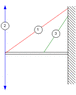
a uniform rod of length 4.0m of mass M is supported by a cable which is under tension T. The other end rests against as wall, where it is held by friction. The coefficient of static friction is 0.5. An additional mass M is hung from the rod at a distance x from the wall
Homework Equations
Mgx + 2 Mg = 4T sinӨ
2Mg = (R/2) + T sin Ө
R = T cos Ө
The Attempt at a Solution
Solve the above three equations simultaneously for Ө = 37 to obtain the minimum value of x in metres where the additional mass M may be hung without causing the rod to slip.
Answer is : x min = 2.8 m
how do you solve this ? I am totally lost :'( please help I have an exam on monday next week :'(