Solving Tension & Pulley Problems: Acceleration & Tension Explained

[amcavoy]

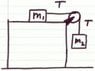
I have attached a picture of what I am describing below (Edit: also a link if the attachment didn't go through):

http://img368.imageshack.us/img368/949/mech036fig012zi.jpg

If a mass m1 sits on top of a frictionless table (assume the pulley is as well), attached to a massless string with a mass m2 on the other end hanging off the table, what is the accel. and tension in the string assuming that m1=2m2?

I figured that if it were attached to a wall (rather than m1), the tension would be |T|=m₂g. However, since the mass m1 will move, this is what I did:

$$\vec{a}=\frac{F}{m}=\frac{m_2g}{m_2+2m_2}=\frac{g}{3}$$

$$T=m\vec{a}=\frac{m_2g}{3}$$

Am I correct?

Thanks for the help

Alex

 

[Doc Al]

However, since the mass m1 will move, this is what I did:
$$\vec{a}=\frac{F}{m}=\frac{m_2g}{m_2+2m_2}=\frac{g}{3}$$

Good!

$$T=m\vec{a}=\frac{m_2g}{3}$$

Careful: $$T = m_1 a$$

Just for the exercise, I recommend doing the problem a second way: Apply Newton's 2nd law to each mass seperately and combine the two equations. (You'll get the same answer, of course.)

 

[Fermat]

The acceleration is correct, but T is the tension, providing acceleration, on m1, not m2.

 

[amcavoy]

The acceleration is correct, but T is the tension, providing acceleration, on m1, not m2.

Hmm... Could you explain a bit more why it isn't m₂? It seems like the hanging mass (m₂) would determine the tension.

Thanks again,

Alex

 

[amcavoy]

Alright I tried your suggestion Doc Al:

$$F_1=\frac{2m_2g}{3}$$

$$F_2=\frac{m_2g}{3}$$

$$F_1+F_2=m_2g$$

I'm not coming up with m₁g like you suggested. Where did I go wrong?

Thank you.

Alex

 

[Doc Al]

Alright I tried your suggestion Doc Al:
$$F_1=\frac{2m_2g}{3}$$
$$F_2=\frac{m_2g}{3}$$
$$F_1+F_2=m_2g$$
I'm not coming up with m₁g like you suggested. Where did I go wrong?

I suggested starting over and looking at each mass separately:

(1) What forces act on mass 1? Write Newton's 2nd law for mass 1.
(1) What forces act on mass 2? Write Newton's 2nd law for mass 2.​

When you do that, you'll get two equations. They will allow you to solve for the acceleration of the masses and the tension in the cord. (And you'll also see why $T = m_1 g$.)

 

[amcavoy]

Edit: Nevermind, I see what you're saying. The force on the mass m1 is equal to the tension, thus T=m1a. Thanks a lot for the help, it's appreciated.

Alex

 

[Doc Al]

You only need to consider the forces parallel to the direction of the acceleration:
on $m_1$: The only horizontal force is the tension in the string
on $m_2$: There two vertical forces, the tension in the string and the weight