Solving Transition of a Gas: Change in Internal Energy & Heat Added/Required

  • Thread starter Thread starter sciontc03
  • Start date Start date
  • Tags Tags
    Gas Transition
sciontc03
Messages
9
Reaction score
0

Homework Statement


I need help with this problem please. My partner and I have stared at this problem and keep going in circles and can't seem to figure out how to work this problem. Please help!

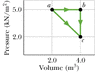
One mole of an ideal diatomic gas undergoes a transition from a to c along the diagonal path in the figure attached.



During the transition, what is the change in internal energy of the gas?

How much energy is added to the gas as heat?

How much heat is required if the gas goes from a to c along the indirect path abc?


Homework Equations



pv=nrt
E=Q-W

The Attempt at a Solution


I don't even know where to begin. Please help.
 

Attachments

  • hrw7_19-23.gif
    hrw7_19-23.gif
    2.1 KB · Views: 476
Physics news on Phys.org
can anybody possibly help me understand this?
 

Thread 'Direction of the magnetic field of an oscillating charge'

Hello everyone, I’m considering a point charge q that oscillates harmonically about the origin along the z-axis, e.g. $$z_{q}(t)= A\sin(wt)$$ In a strongly simplified / quasi-instantaneous approximation I ignore retardation and take the electric field at the position ##r=(x,y,z)## simply to be the “Coulomb field at the charge’s instantaneous position”: $$E(r,t)=\frac{q}{4\pi\varepsilon_{0}}\frac{r-r_{q}(t)}{||r-r_{q}(t)||^{3}}$$ with $$r_{q}(t)=(0,0,z_{q}(t))$$ (I’m aware this isn’t...
View full post »

Thread 'Initial conditions for orbits around a wormhole'

Hi, I had an exam and I completely messed up a problem. Especially one part which was necessary for the rest of the problem. Basically, I have a wormhole metric: $$(ds)^2 = -(dt)^2 + (dr)^2 + (r^2 + b^2)( (d\theta)^2 + sin^2 \theta (d\phi)^2 )$$ Where ##b=1## with an orbit only in the equatorial plane. We also know from the question that the orbit must satisfy this relationship: $$\varepsilon = \frac{1}{2} (\frac{dr}{d\tau})^2 + V_{eff}(r)$$ Ultimately, I was tasked to find the initial...
View full post »

Similar threads

DeltaG and DeltaA calculation for heating a gas at constant volume
Replies
3
Views
2K
Phase transitions in a superconductor
Replies
5
Views
2K
Heat engine undergoing an elliptical cycle
Replies
5
Views
2K
Adding heat to a Non Ideal Gas problem
Replies
5
Views
2K
Heating a room and internal energy question
Replies
2
Views
2K
Internal Energy of an Ideal Gas
Replies
4
Views
2K
I Focus Problem for Entropy Change in Irreversible Adiabatic Process
2
Replies
60
Views
9K
Thermo - double Vrms, find heat required
Replies
2
Views
2K
I Irreversible adiabatic processes & entropy change (clarification needed)
Replies
22
Views
5K
Solving Thermodynamics Ideal Gas Probs: Q, W, ΔU w/Help | Physicsforums.com
Replies
1
Views
2K

Hot Threads

Recent Insights

Back
Top