Solving Two-Pendulum Collision: Find Max Angle

[ProBasket]

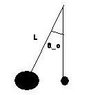
Two simple pendulums of equal length (L=40cm) are suspended from the same point. The pendulum bobs are point-like masses of m1=450g and m2=150g. the more massive bob (m1) is initially drawn back at an angle of \theta_0 = 40^o from vertical, as shown(in attached pic). After m1 is released it swings down to \theta = 0 where it collisdes with m2 and the masses stick together. I have the answers to the following problems, but i would like to know how to do it.

a.) Find the speed of m1 just before the collision. this one was pretty simple, the answer was 1.35m/s and it matches the answer given.

b.) Determind the maximum angle to which the masses swing after the collision. well from problem a.) i found that v_i = \sqrt{2gL(1-cos(45))}

when the bigger mass hits the smaller mass, U_o = mgL(1-cos(\theta)) right? and K_o = 0. at the end of the collision, K_f = 1/2mv^2 and U_f = 0. which means v_{2f}^2 = 2gL(1-cos(\theta_2)) right?

well plugging everything i know to V_{2f}^2 = (\frac{(2*m_1)}{m_1+m_2})^2*v_i^2 m1 = 450 and L = .4 m right? i get V_{2f}^2 = 4.1

then setting 4.1 equal to v_2f 4.1 =2gL(1-cos(\theta_2)) and solving for theta, i get 61 degrees. but the real answer is 27, what did i do wrong?

 

[einstone]

Unlike the total momentum,the total energy is not conserved during this inelastic collision.
Regards,
Einstone.

 

[HallsofIvy]

You say the larger mass is held at 40 degrees in the statement of the problem but use 45 degrees later. Since "Frogpad", giving essentially the same problem in a different post uses 40 degrees, I am going to assume that is correct.

Raising the mass on a 40 cm pendulum arm by 40 degrees means it is raised 40(1- cos(40)) cm vertically and so has potential energy 450g(40(1- cos(40))= 4131186 ergs(g here is the acc due to gravity- 981 cm/s²- rather than "grams") relative to its original position. Just before it strikes the second weight, it is back to its original position and so has 0 potential energy. All the potential energy has been converted to kinetic energy: its kinetic energy is 4131186 ergs. Since kinetic energy is (1/2)mv²= 4131186, we have v²= 8262374/450= 18360 so
v= 135.5 cm/s, just what you got!

Now the two masses stick together so we can think of that as a single mass of 450+350= 800 g. As einstone said, since this is not an elastic collision,energy is not conserved and but momentum is: the initial momentum of the system was the momentum of the first mass (450 g)(135.5 cm/s)= 60976 dynes. The momentum after the collision (800 g)(v cm/s)= 60976 so v= 60976/800= 76.3 cm/s.

Now, calculate the kinetic energy of an 800 g mass moving at 76.3 cm/s. Find the height and then angle that will give potential energy for an 800 g mass equal to that kinetic energy. The difference between that and the original kinetic energy (= original potential energy) is the change in energy due to the collision.