sukharef
- 54
- 0
Hello!
I've got unexpected problems with this very integral.
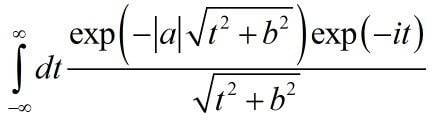
I've looked through "gradshteyn and ryzhik" and found similar, but not the same. So the result, as i think, will be Bessel functions or so. Wolfram Mathematica could not calculate it, so i thought you would help with it, because it does not seem to be very difficult.
Thank you in advance!
I've got unexpected problems with this very integral.
I've looked through "gradshteyn and ryzhik" and found similar, but not the same. So the result, as i think, will be Bessel functions or so. Wolfram Mathematica could not calculate it, so i thought you would help with it, because it does not seem to be very difficult.
Thank you in advance!