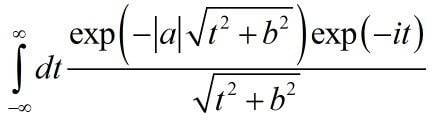Solving Unexpected Integral Problem with Bessel Functions

  • Context: Graduate 
  • Thread starter Thread starter sukharef
  • Start date Start date
  • Tags Tags
    Integral Specific
Click For Summary

Discussion Overview

The discussion revolves around an integral involving Bessel functions that a participant finds unexpectedly challenging. The scope includes theoretical exploration and mathematical reasoning related to the integral's properties and potential transformations.

Discussion Character

  • Exploratory
  • Technical explanation
  • Mathematical reasoning
  • Debate/contested

Main Points Raised

  • One participant suggests that the integral may yield results involving Bessel functions, specifically ##\pi \mathrm{i} H_0^1 ( \mathrm{i} b |a| )## or ##2K_0 (b |a| )##, referencing prior work by Duran, Muga, and Nedelec.
  • Another participant expresses uncertainty about the transformations mentioned and questions whether specific polar coordinates are involved, indicating that the integral might be more complex than initially thought.
  • There is a discussion about the singularities present in the integral, with one participant noting that their integral has a singularity on the real axis, contrasting with the reference integral.
  • Participants explore the relationship between parameters in the integral, suggesting that ##|a|## corresponds to certain variables and questioning the appropriateness of the transformations for their specific case.
  • One participant proposes that the conversion might not fit the problem due to assumptions made about the parameters, particularly regarding the nature of ##b## and ##k##.
  • Another participant suggests that in the case where ##a=0##, the result would simplify to ##2K_0(b)##, indicating a preference for this function over others in the context of their integral.

Areas of Agreement / Disagreement

Participants express differing views on the applicability of certain transformations and the nature of singularities in their integrals. There is no consensus on the best approach or the correctness of the proposed results, indicating ongoing debate and exploration.

Contextual Notes

Participants note that the integral's complexity may depend on specific assumptions and definitions, particularly regarding the parameters involved and their implications for the transformations discussed.

sukharef
Messages
54
Reaction score
0
Hello!
I've got unexpected problems with this very integral.
f551f55ddf15.jpg

I've looked through "gradshteyn and ryzhik" and found similar, but not the same. So the result, as i think, will be Bessel functions or so. Wolfram Mathematica could not calculate it, so i thought you would help with it, because it does not seem to be very difficult.

Thank you in advance!
 
Physics news on Phys.org
I'm interested to hear what you are working on.
I have dealt with that specific integral myself and found a reference showing that it is equivalent to
##\pi \mathrm{i} H_0^1 ( \mathrm{i} b |a| ) ## or ## 2K_0 (b |a| ).##
The constants may be off...but I am pretty sure about the result.
Duran, Muga, and Nedelec use a transformation in "The Helmholtz equation in a locally perturbed half-plane with passive boundary." IMA Jrnl. of Appl. Math. 2006.
Which fits the forms you will find in Gradshteyn and Ryzhik.
This method was used by Van and Wood in, "A Time-Domain Finite Element Method for Helmholtz Equations." Jrnl. of Comp. Phys. 2002.
I hope this is helpful...I could not actually do the transformations myself, so I had to rely on some smart folks who had done it before me.
 
  • Like
Likes   Reactions: sukharef
RUber said:
I'm interested to hear what you are working on.
I have dealt with that specific integral myself and found a reference showing that it is equivalent to
##\pi \mathrm{i} H_0^1 ( \mathrm{i} b |a| ) ## or ## 2K_0 (b |a| ).##
The constants may be off...but I am pretty sure about the result.
Duran, Muga, and Nedelec use a transformation in "The Helmholtz equation in a locally perturbed half-plane with passive boundary." IMA Jrnl. of Appl. Math. 2006.
Which fits the forms you will find in Gradshteyn and Ryzhik.
This method was used by Van and Wood in, "A Time-Domain Finite Element Method for Helmholtz Equations." Jrnl. of Comp. Phys. 2002.
I hope this is helpful...I could not actually do the transformations myself, so I had to rely on some smart folks who had done it before me.

Thank you!
I'm trying to calculate radiation arises when a particle moves along the shaped surface.
I've looked through the articles and i want to know what transformation do you exactly mean, specific polar coordinates?
I guess if the result would be πiH10(ib|a|) or 2K0(b|a|) Wolf.Mathematica would calculate it in terms of these functions. Maybe it's not that simple.
 
The explanation of the parametrization is in the Duran article.
upload_2015-8-19_2-31-37.png
 
RUber said:
The explanation of the parametrization is in the Duran article.
View attachment 87518
are you sure about the title of the article? i can not find that piece that you are referring to.
besides the integral (10) has a singularity on Re axis, not on I am like mine one has.
 
sukharef said:
are you sure about the title of the article? i can not find that piece that you are referring to.
besides the integral (10) has a singularity on Re axis, not on I am like mine one has.

I think the paper in Ref. 5 here:

http://cib.epfl.ch/Rappaz60/programme/JeanClaudeNedelec.pdf

and

http://imamat.oxfordjournals.org/content/71/6/853.abstract

is the paper referred to by RUber above, I believe.
 
Last edited by a moderator:
Last edited by a moderator:
In your integral, |a| holds the same place as |x_2 - y_2| and your b^2 = -k^2, or b = ik, and (x_1 - y_1) = 1.
r would be ##\sqrt{a^2 + 1}## k= -ib.
So, would ## iH_0^1(ib\sqrt{a^2 + 1})## work?
I might be glossing over the assumption that k>0 that was made.

I think you are right...this conversion might not fit your problem.
You mentioned the singularity in the complex plane. Is b complex?
 
RUber said:
In your integral, |a| holds the same place as |x_2 - y_2| and your b^2 = -k^2, or b = ik, and (x_1 - y_1) = 1.
r would be ##\sqrt{a^2 + 1}## k= -ib.
So, would ## iH_0^1(ib\sqrt{a^2 + 1})## work?
I might be glossing over the assumption that k>0 that was made.

I think you are right...this conversion might not fit your problem.
You mentioned the singularity in the complex plane. Is b complex?
no, b and a are real. i meant that k = +-ib.
 
  • #10
RUber said:
In your integral, |a| holds the same place as |x_2 - y_2| and your b^2 = -k^2, or b = ik, and (x_1 - y_1) = 1.
r would be ##\sqrt{a^2 + 1}## k= -ib.
So, would ## iH_0^1(ib\sqrt{a^2 + 1})## work?
I might be glossing over the assumption that k>0 that was made.

I think you are right...this conversion might not fit your problem.
You mentioned the singularity in the complex plane. Is b complex?
i think 2K0() is more appropriate here, because in particular case of a=0, the result will be 2K0(b)
 

Similar threads

Graduate Integral of 2 Bessel functions of different orders
  • · Replies 3 ·
Replies
3
Views
2K
Symbolic integration of a Bessel function with a complex argument
  • · Replies 5 ·
Replies
5
Views
4K
Graduate Memory issues in numerical integration of oscillatory function
  • · Replies 3 ·
Replies
3
Views
2K
Graduate Coulomb integrals of spherical Bessel functions
  • · Replies 10 ·
Replies
10
Views
3K
Undergrad Should the function f to be continuous for applying MVTI or not?
  • · Replies 4 ·
Replies
4
Views
2K
Undergrad Did Math DF's integral calculator make a glaring mistake?
  • · Replies 8 ·
Replies
8
Views
3K
Graduate Heat conduction equation in cylindrical coordinates
  • · Replies 2 ·
Replies
2
Views
3K
Graduate Double Integration of Bessel Functions
  • · Replies 10 ·
Replies
10
Views
4K
Graduate Integrating a function of which poles appear on the branch cut
  • · Replies 1 ·
Replies
1
Views
2K
Graduate Help needed with derivation: solving a complex double integral
  • · Replies 1 ·
Replies
1
Views
2K