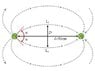
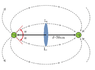
The discussion revolves around calculating the electric flux through a disk due to two charges, focusing on the definitions and properties of electric field lines. Participants clarify the direction of the electric field and how it relates to the field lines, emphasizing that the electric flux through the disk is influenced by both charges. The equations for electric flux are presented, with specific attention to the contributions from each charge and the geometry of the setup. Ultimately, the correct answer for the flux calculation is confirmed as 30.52 cm, highlighting the effectiveness of the discussed methods. The conversation showcases a collaborative problem-solving approach in physics.