Sphere resting on a vertical wall

[zorro]

Homework Statement

Weight of sphere = W and a force P is applied on its surface to attain equilibrium (Friction is present). Then

1. Pmin = √3W/2
2. Pmin = (√5-1)W/2
3. When P is minimum, Angle of friction max between sphere and wall is cos^-1 (√5-1)/2
4. When P is minimum, Angle of friction max between sphere and wall is tan^-1 (√3-1)/(√5-1)

The Attempt at a Solution

For translational equilibrium,
W=(mu)P

I can't find a valid equation for rotational equilibrium.
Help

 

[pongo38]

The question is unclear to me.

 

[zorro]

What is unclear to you?

 

[pongo38]

1. Pmin = √3W/2
2. Pmin = (√5-1)W/2

What do your two lines 1. and 2. mean? Why are they different? What is the direction of the restraining force?

 

[zorro]

This is a Multiple Choice Question (with more than one correct answer)

1. and 2. are simply different choices. You have to find out the correct choice.

Obiviously, the direction of the force applied P will be perpendicular to the surface ( we have to assume that its line of action passes through the centre of mass of the sphere)

 

[pongo38]

This is a Multiple Choice Question (with more than one correct answer)

1. and 2. are simply different choices. You have to find out the correct choice.

Obiviously, the direction of the force applied P will be perpendicular to the surface ( we have to assume that its line of action passes through the centre of mass of the sphere)

I didn't get it that it was multiple choice. Ok. I don't think you can assume that theline of action of P passes through the centre of the sphere. For rotational equilibrium (I assume you mean that the sum of moments about any point must be zero) all the forces acting on the sphere must be concurrent or parallel. I suggest you draw a free body diagram with all the forces acting on the sphere.

 

[zorro]

Ok then, here is my approach-
Let the force P be applied at a distance x above the centre of mass.
For rotational equilibirum about the centre of mass,
Px = fR = \muPR ( since N=P )
i.e. \mu = x/R

Now for translational equilibrium, f = W
i.e. Px/R = W
or P = WR/x

Minimising this function would not give a valid result.

 

[hikaru1221]

The friction coef. is not given? Without it, no numerical value can be drawn I think. For example, when mu->0, P certainly is W; when mu->inf, just with a very small P, friction is large enough to hold the sphere.
By the way, I don't think the conclusion that P is horizontal is correct. P can have a vertical component to help lessening friction, which also means lessening normal force & thus horizontal component of P and P in total.

 

[zorro]

mu is certainly > 0
Yes P can also have a vertical component.
I think the question is unclear...

 

[hikaru1221]

What I meant is that P(min) can take any value depending on mu. Say if mu is very small, then P is approximately equal to W. You should check the question again.
If you write all the equations including P(vertical), you will arrive at: P_{min}=\frac{W}{\sqrt{1+\mu^2}}
That occurs when tan\phi = \mu. That means: \phi = \alpha=tan^{-1}\mu and \vec{P}_{min} is a reflection of \vec{R} through vertical axis through center of the sphere.

 

[zorro]

I did not understand what do you mean by reflection of P_min.

Do you mean these equations-
Pcos\phi + Rcos \alpha + f = W
N = Rsin \alpha - Psin\phi

 

[hikaru1221]

Sorry, I was wrong earlier. This problem is tougher than I thought. At this time, I haven't arrived at the exact answer yet. Anyway just some thoughts:

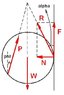
\vec{R} = \vec{F} + \vec{N} is the sum of frictional force and normal force, i.e. it is the force exerted by the wall. The torque balance condition leads to that \vec{P} , \vec{W} and \vec{R} must be concurrent.

From the force balance condition:
Pcos\phi + F = W
Psin\phi = N
We also have: F\leq \mu N

Therefore: P \geq \frac{W}{\mu sin\phi + cos\phi}

Since \mu = const , after doing some math, we arrive at:

P \geq \frac{W}{\mu sin\phi + cos\phi} \geq \frac{W}{\sqrt{1+\mu^2}} .

So with that assumption, we have: P=P_{min}=W/\sqrt{1+\mu^2} when tan\phi = \mu and friction is maximum (F=uN). When friction is max, cot\alpha = \mu and thus tan\phi = cot\alpha . With this relation between 2 angles, plus the concurrency condition found earlier, we can see that \vec{P} is perpendicular to \vec{R} (not reflection!) - See picture 1.

Now here comes the trouble: As \vec{P} must be exerted on the lower leftmost quarter of the sphere, and \vec{P} is perpendicular to \vec{R} , we can see that the point of concurrency M can only move in the range from C, center of the sphere, to T, top point of the sphere. That corresponds to a range of value of \alpha and thus \mu , as \mu = cot\alpha: 45^o \leq \alpha \leq 90^o and 0 \leq \mu \leq 1. That means, the result we've got can only apply to cases where 0 \leq \mu \leq 1!

In practice, normally, 0< \mu < 1. However the case \mu > 1 does exist. And this is where I'm completely stumped. If we return back to the first few equations, we can see that these will hold for any cases (as long as there is equilibrium):

(1) P \geq \frac{W}{\mu sin\phi + cos\phi} \geq \frac{W}{\sqrt{1+\mu^2}}

(2) cot\alpha \leq \mu

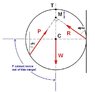
The concurrency condition leads to another equation - see picture 2:

R = dtan\alpha

\frac{sin(\theta - \phi)}{d} = \frac{sin\phi}{R}

Thus: (3) sin(\theta - \phi)tan\alpha = sin\phi

And a restriction of the position of \vec{P}: (4) 0^o \leq \theta \leq 90^o

Now you have a bunch of equations + inequalities. Solving them is not an easy task. Wanna try?

 

[zorro]

\vec{R} = \vec{F} + \vec{N} is the sum of frictional force and normal force, i.e. it is the force exerted by the wall. The torque balance condition leads to that \vec{P} , \vec{W} and \vec{R} must be concurrent.

I don't get that.
If we consider the net torque about COM,
Pd₁ = Rd₂ (d₁ and d₂ are perpendicular distances from COM)

How do we conclude that the three forces must be concurrent?

Even if we don't use the concurrency condition, we get
tan\phi = cot\alpha
and using slopes of both the lines we find that they are perpendicular.

 

[hikaru1221]

I don't get that.
If we consider the net torque about COM,
Pd₁ = Rd₂ (d₁ and d₂ are perpendicular distances from COM)

How do we conclude that the three forces must be concurrent?

Suppose that \vec{W} meets \vec{R} at point A. Therefore, their torques about this point are zero. The torque about A of the only force left, \vec{P}, must also be zero, i.e. \vec{P} also has to pass through A. Therefore, the 3 vectors are concurrent.

Notice that this only applies to a system of 3 forces. If there is another 4th force \vec{Q}, then that sum of torques about A of \vec{P} and \vec{Q} is zero doesn't result in that torque about A of \vec{P} alone is zero.

Even if we don't use the concurrency condition, we get
tan\phi = cot\alpha
and using slopes of both the lines we find that they are perpendicular.

What I meant is that the result should be that they are perpendicular, not reflection.

The concurrency condition, plus the fact that \vec{P} and \vec{R} are perpendicular to each other, leads to that the intersection point M of \vec{P} and \vec{R} must lie on the vertical line joining C and T (so that \vec{W} also goes through M).

 

[zorro]

Thanks a lot hikaru1221 ( I wrote the numbers too )