Tanya Sharma
- 1,541
- 135
Sphere slipping against blocks
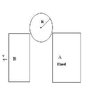
In the given arrangement ,a sphere of radius R is placed on the two blocks A and B where A is fixed and B is moving at a constant speed ‘v’ towards left .Find the speed of the sphere’s center when the distance between the blocks is √R and the sphere’s center is at a vertical distance √R from the top of the blocks .All surfaces are frictionless .
Ans : v/2
Let the distance between the blocks be 'y' at any instant.
Let the distance between the sphere’s center be at a vertical distance 'x' from the top of the blocks .
Let the horizontal distance between B and sphere's center O be 'l' .
Then l=y/2 .
Differentiating we get,dl/dt = (1/2)dy/dt = v/2
From the geometry of the setup , x2 + l2 = R2
Differentiating , we get dx/dt = -(l/x)dl/dt .
Now when x=√R and y=√R (i.e l=√R/2) ,we have dx/dt = -v/4 i.e the horizontal speed of O is v/4 downwards .
The center also has a horizontal speed v/2 towards left.
The net speed of the center is (√5/4)v which is incorrect .
I would be grateful if someone could help me with the problem .
Homework Statement
In the given arrangement ,a sphere of radius R is placed on the two blocks A and B where A is fixed and B is moving at a constant speed ‘v’ towards left .Find the speed of the sphere’s center when the distance between the blocks is √R and the sphere’s center is at a vertical distance √R from the top of the blocks .All surfaces are frictionless .
Ans : v/2
Homework Equations
The Attempt at a Solution
Let the distance between the blocks be 'y' at any instant.
Let the distance between the sphere’s center be at a vertical distance 'x' from the top of the blocks .
Let the horizontal distance between B and sphere's center O be 'l' .
Then l=y/2 .
Differentiating we get,dl/dt = (1/2)dy/dt = v/2
From the geometry of the setup , x2 + l2 = R2
Differentiating , we get dx/dt = -(l/x)dl/dt .
Now when x=√R and y=√R (i.e l=√R/2) ,we have dx/dt = -v/4 i.e the horizontal speed of O is v/4 downwards .
The center also has a horizontal speed v/2 towards left.
The net speed of the center is (√5/4)v which is incorrect .
I would be grateful if someone could help me with the problem .
Attachments
Last edited:
 .
.